Частотные характеристики. Частотные характеристики получают при гармоническом входном воздействии, заданном либо в тригонометрической форме

Частотные характеристики получают при гармоническом входном воздействии, заданном либо в тригонометрической форме

,

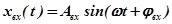либо в комплексной форме

,

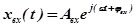где А_вх – амплитуда;

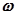- круговая частота;

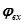- начальная фаза входного сигнала.

При этом выходной сигнал изменяется также по гармоническому закону (см. рис. 2.6) с той же частотой 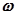, но с другой амплитудой А_вых и начальной фазой :

,

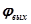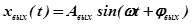или

.

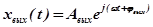Зависимость отношения комплексной амплитуды 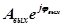выходного сигнала к комплексной амплитуде 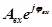входного сигнала от частоты колебаний называют частотной функцией:

,

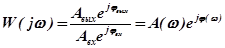где 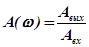- модуль частотной функции, или амплитудно-частотная характеристика (АЧХ);

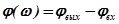- аргумент частотной функции, или фазо-частотная характеристика (ФЧХ).

Частотная характеристика может быть представлена на комплексной плоскости, если предварительно представить частотную функцию в виде:

,

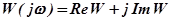где 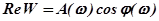- действительная часть частотной функции;

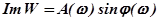- мнимая часть частотной функции.

Частотная характеристика на комплексной плоскости называется амплитудно-фазовой частотной характеристикой (АФЧХ). Частотная функция может быть получена из выражения для передаточной функции W(s), представляющей собой отношение изображений по Лапласу выходной величины 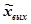и входной величины 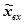при нулевых начальных условиях:

.

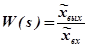Для получения передаточной функции достаточно в дифференциальном уравнении системы произвести замену операции дифференцирования 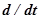на оператор Лапласа s, входную х_вх и выходную х_вых величины представить их изображениями по Лапласу 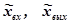и решить это уравнение относительно 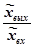. Если в выражении для W(s) заменить s на jw, то получим частотную функцию W(jw) системы.

Теоретическое исследование частотных характеристик связано с приведением дифференциальных уравнений к записи их в операторной форме, определением и анализом передаточной и частотной функций звеньев.