2015-05-13
269
Звено описывается дифференциальным уравнением:
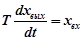(2.7)
Передаточная функция звена:
.
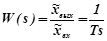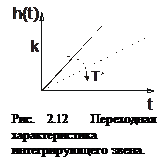
Переходная функция интегрирующего ТЗ определяется в результате интегрирования левой и правой частей дифференциального уравнения (2.7) при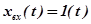 
и имеет следующий вид (рис. 2.12):
.
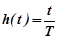Переходная характеристика интегрирующего ТЗ представляет собой нарастающую наклонную прямую, темп нарастания которой зависит от постоянной времени Т. Чем меньше Т, тем быстрее протекает переходный процесс. В отличие от переходных характеристик других ТЗ переходная характеристика интегрирующего ТЗ не стремится к какому-либо значению, а все время имеет нарастающий характер.
Частотная функция интегрирующего ТЗ определяется выражением:
.
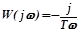АЧХ и ФЧХ интегрирующего звена (рис. 2.13,а и 2.13,б соответственно):
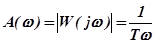
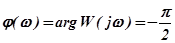
АЧХ интегрирующего звена представляет собой гиперболу. Чем выше частота колебаний, тем меньше амплитуда колебаний выходного сигнала. При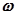 
= 0 амплитуда выходного сигнала равна бесконечности. Начальная фаза выходных колебаний отстает от начальной фазы входных колебаний на угол 
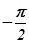и не зависит от частоты колебаний.
АФЧХ интегрирующего ТЗ совпадает с отрицательной частью мнимой оси (рис. 2.13,в). Точка, соответствующая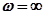 
, расположена в начале координат.
