2015-05-13
352
Пусть намечается строительство нового предприятия при следующих условиях.
- Выпуск продукции связан с эксплуатационными расходами, которые имеют нормальное распределение с заданными параметрами: математическим ожиданием расхода
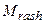и среднеквадратическим отклонением расхода 
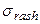. - Емкость рынка, где должна реализоваться продукция предприятия, имеет нормальное распределение с заданными параметрами: математическим ожиданием емкости рынка
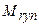и среднеквадратическим отклонением емкости рынка 
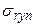. - Доля предприятия в рынке является неопределенной и может быть задана некоторой произвольной функцией распределения (например, кусочно-равномерной функцией).
- Случайная прибыль предприятия определяется по следующей зависимости:
Prof=Ryn×Dol-Rash,
где Ryn – случайная величина емкости рынка;
Dol – случайная величина доли предприятия на рынке;
Rash – случайная величина эксплуатационных расходов предприятия.
Выходные характеристики модели:
- сумма случайных величин прибыли для
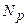случайных реализаций 
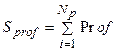; - сумма квадратов случайных величин прибыли для 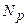случайных реализаций
.
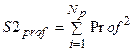Показатель эффективности: минимальная гарантированная прибыль, определяемая по формулам:
;
;
,
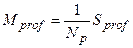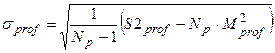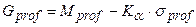где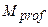 
– математическое ожидание прибыли;
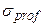– среднеквадратическое отклонение прибыли;
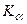– квантиль нормального распределения, соответствующий заданному уровню гарантии a ( 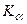=1,28 при a=0,9);
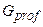– минимальная гарантированная прибыль.
Варьируемые переменные: параметры кусочно-равномерного распределения доли предприятия в рынке.
Роль степени неопределенности при описании доли предприятия в рынке. С увеличением степени неопределенности при описании доли предприятия в рынке средняя прибыль растет, однако минимальная гарантированная прибыль уменьшается из-за увеличения разброса случайной величины прибыли.
«Паутинообразная» модель фирмы
Общие представления о «паутинообразных» моделях фирмы. Такие модели создаются для решения проблемы, как будет вести себя цена на товар при изменении объема производства. Общий принцип заключается в том, что при увеличении производства происходит падение спроса и приходится снижать цену. Возникает вопрос, при каких условиях цена будет стабильной? В литературе описано несколько вариантов такой модели. Все они обладают определенными одинаковыми свойствами. Обычно в них предполагается, что спрос на некоторый продукт (чаще всего рассматривается сельскохозяйственная продукция) на заданном отрезке времени зависит от цены (и других факторов) на этом отрезке. Что же касается предложения, то оно определяется ценами предыдущего периода времени (недели, месяца, квартала и т.д.). Кроме того, предполагается, что рынок всегда находится в условиях локального равновесия. Исторически такая модель получила название «паутинообразной», вероятно, потому, что такого же принципа «учета предыдущего шага» придерживается паук, когда он ткет паутину.
