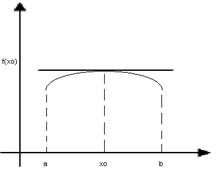
Теорема Ферма. Если ф-я y=f(x) определена на интервале (a,b) и в некоторой внутренней точке x0 (из (a,b)) принимает наибольшее или наименьшее значение, то производная ф-и в этой точке (если она вообще сущ-ет) равна 0.
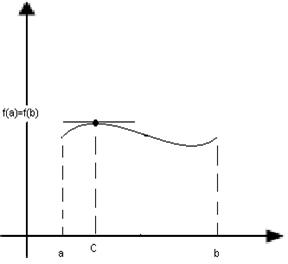 Замечание. Теорема неверна, если ф-я рассматривается на отрезке, где она достигает наибольшее (наименьшее) значение на одном из концов.
Замечание. Теорема неверна, если ф-я рассматривается на отрезке, где она достигает наибольшее (наименьшее) значение на одном из концов.
Теорема Ролля. Пусть ф-я y=f(x):
1)определена и непрерывна на отрезке [a,b]
2)существует ее производная на интервале (a,b)
3)на концах отрезка принимает равные значения, т.е. f(a)=f(b).
Тогда внутри отрезка существует по крайней мере одна такая точка с (принадл (a,b)), в которой производная ф-и равна 0 (f’(c)=0)
Если условия теоремы выполняются, то в точке кривой с ф-и f(c) касательная параллельна оси Ox.
 Замечание: каждое из условий теоремы явл необходимым.
Замечание: каждое из условий теоремы явл необходимым.
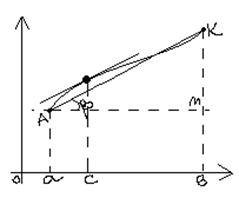
Теорема Лагранжа. Пусть ф-я y=f(x):
1)определена и непрерывна на отрезке [a,b]
2)существует производная ф-и на интервале (a,b).
Тогда между точками a и b найдется точка с, в которой выполняется равенство 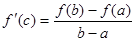 .
.
К графику: f(b)-f(a)=MK, b-a=AM, 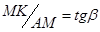
Теорема Коши. Пусть ф-и y=f(x) и g(x):
1) непрерывна на отрезке [a,b]
2) существуют конечные производные ф-й на интервале (a,b)
3) g’(x) не равна 0 на (a,b)
тогда внутри отрезка существует по крайней мере одна такая точк5а с (принадл (a,b)), в которой выполняется равенство 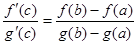
 2015-05-13
2015-05-13 5497
5497








