Формула Тейлора для многочлена: 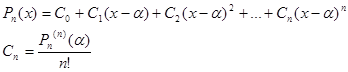
Теорема Тейлора. Пусть ф-я у=f(x) определена в некоторой точке х=а и в некоторой окрестности этой точки ф-я имеет производные до (n+1)-го порядка, тогда сущ-ет х=ξ, такая, что выполняется формула Тейлора:
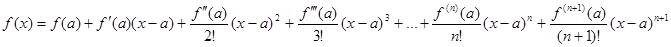 ,
,
Причем точка ξ лежит между х и а, т.е. ξ=а+α(х-а) и 0<α<1.
Последнее слагаемое в формуле Тейлора называется остаточным членом в форме Лагранжа и обозначается 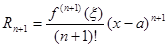 .
.
Сущ-ет так же остаточный член в форме Пеано, который обозначается: 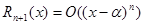 .
.
При а=0 формула Тейлора называется формулой Маклорена:
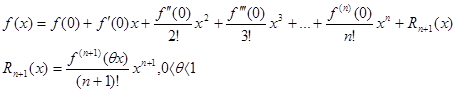
Пример.
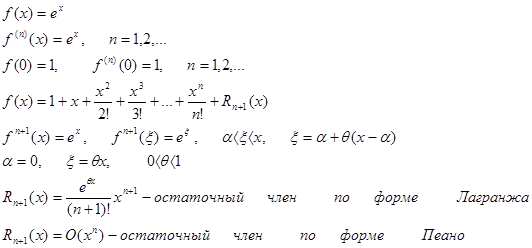
 2015-05-13
2015-05-13 1262
1262
