Теорема Лейбница (достаточный признак сходимости знакочередующегося ряда)

Дан знакочередующийся ряд .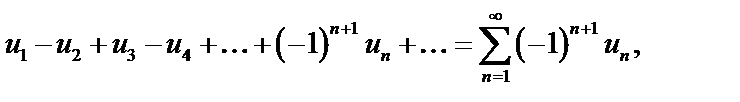

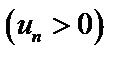Если 1)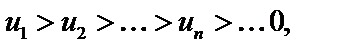

2) .

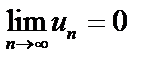Тогда ряд 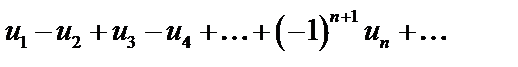сходится, причем его сумма .

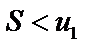Пример. Исследовать на сходимость ряд .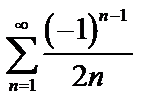

Решение: Данный ряд является знакочередующимся.

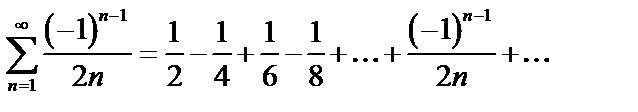
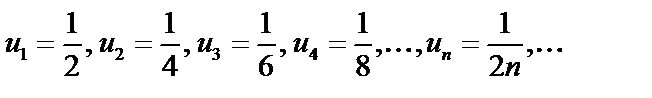
Проверим выполнение условий признака Лейбница.

1) .

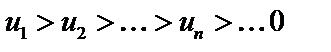Действительно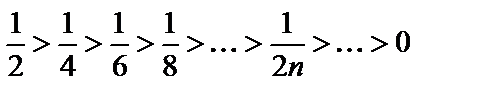

2) .

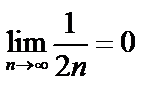Следовательно, по признаку Лейбница ряд сходится.

Теорема (достаточный признак сходимости знакопеременных рядов). Дан знакопеременный ряд 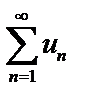. Если ряд 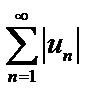сходится, то исходный ряд 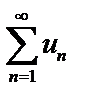тоже сходится.