Ряд, членами которого являются функции от «x» называются функциональным 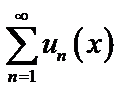 .
.
Совокупность значений «x», при которых ряд 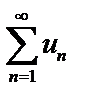 сходится, называется областью сходимости функционального ряда.
сходится, называется областью сходимости функционального ряда.
В частности, функциональный ряд вида: 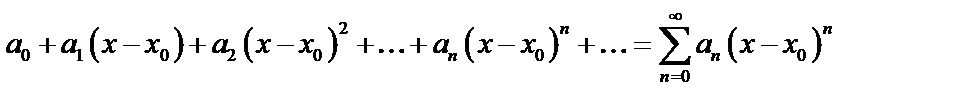 , где
, где 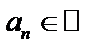 , называется степенным рядом.
, называется степенным рядом.
Доказано, что для любого степенного ряда существует интервал сходимости с центром в точке 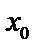 и некоторым радиусом
и некоторым радиусом 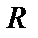 , внутри которого ряд сходится, вне расходится, а на концах интервала сходимости в точках
, внутри которого ряд сходится, вне расходится, а на концах интервала сходимости в точках 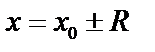 различные степенные ряды ведут себя по-разному.
различные степенные ряды ведут себя по-разному.
| ? |
| ? |
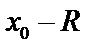
|
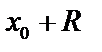
|
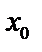
|
| расходится |
| расходится |
| сходится |
| R |
| R |
Для отыскания интервала сходимости можно использовать формулу 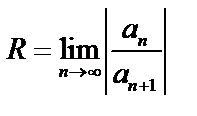 , но только, если среди коэффициентов
, но только, если среди коэффициентов 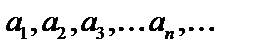 нет равных нулю. Поэтому для любых степенных рядов интервал сходимости можно находить другим путем, применяя признак Даламбера к ряду, составленному из абсолютных величин членов исходного ряда.
нет равных нулю. Поэтому для любых степенных рядов интервал сходимости можно находить другим путем, применяя признак Даламбера к ряду, составленному из абсолютных величин членов исходного ряда.
Предлагается следующий план нахождения области сходимости для любого степенного ряда:
1. Применяя признак Даламбера к ряду 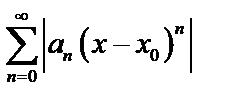 , находим «l» (
, находим «l» (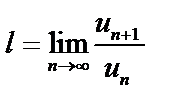 )
)
2. Решая неравенство 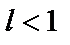 , находим интервал сходимости, в центре которого обязательно должна быть точка
, находим интервал сходимости, в центре которого обязательно должна быть точка 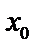 .
.
3. Исследуем поведение исходного ряда в концевых точках интервала сходимости.
4. Записываем ответ (т.е. указываем область сходимости).
Пример. Найти область сходимости степенного ряда: 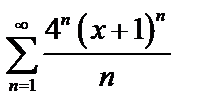 .
.
Решение:
1. Составим ряд из модулей членов данного ряда и применим к нему признак Даламбера 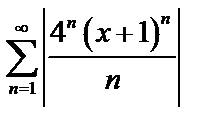 ;
; 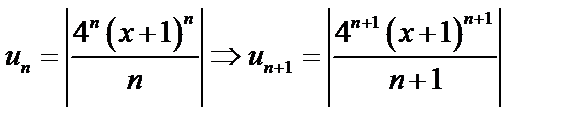 .
.
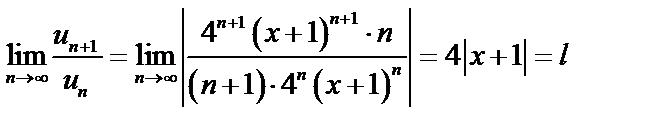 .
.
2. При 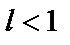 ряд из модулей (а, значит, и исходный) сходится, т.е. надо решить неравенство:
ряд из модулей (а, значит, и исходный) сходится, т.е. надо решить неравенство: 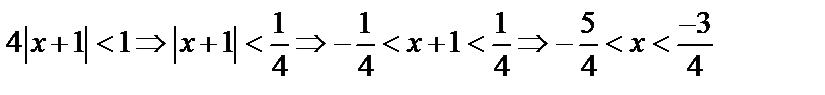
| ? |
| ? |
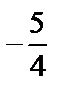
|
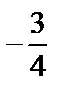
|
| -1 |
| расходится |
| расходится |
| сходится |
3. Исследуем исходный ряд на сходимость в точках 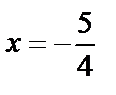 и
и 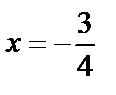 .
.
При 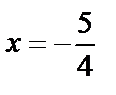 имеем
имеем 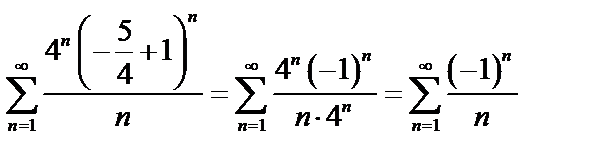 .
.
Ряд знакочередующийся, применим к нему признак Лейбница.
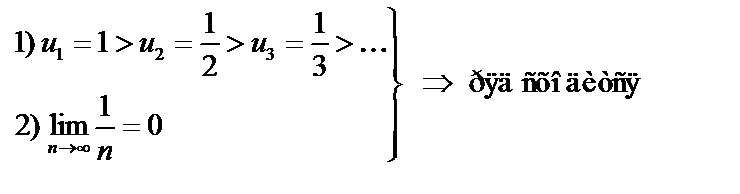
Точка 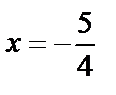 входит в область сходимости.
входит в область сходимости.
При 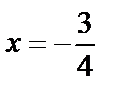 имеем
имеем 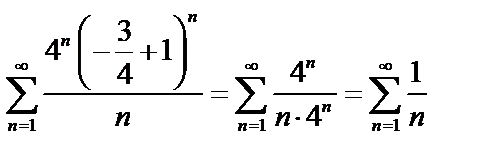 .
.
Так как ряд 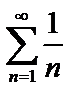 – гармонический,
– гармонический, 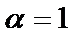 , то он расходится, а значит точка
, то он расходится, а значит точка 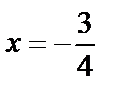 в область сходимости не входит.
в область сходимости не входит.
4. Ответ: область сходимости: 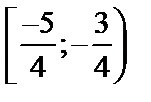 .
.
 2015-05-13
2015-05-13 476
476








