Замечания

1. Члены тригонометрического ряда имеют общий период .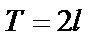

2. При 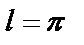тригонометрический ряд имеет вид

,

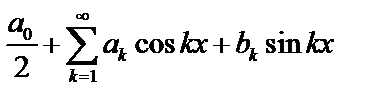при этом общий период членов ряда .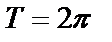

Членами ряда Фурье являются гармоники 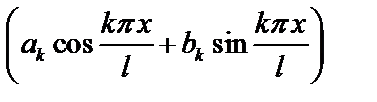с амплитудой 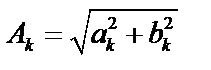и частотой .

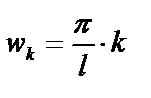Теорема Дирихле. Если периодическая функция 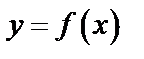с периодом 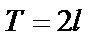на любом промежутке длиной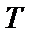

а) кусочно-непрерывна, т.е. непрерывна или имеет конечное число точек разрыва первого рода;

б) кусочно-монотонна или имеет конечное число экстремумов, то эту функцию можно представить рядом Фурье, который сходится на всей числовой оси, и его сумма:

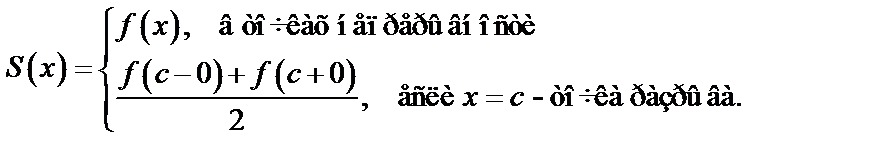
Пусть функция 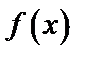удовлетворяет условиям теоремы Дирихле, тогда

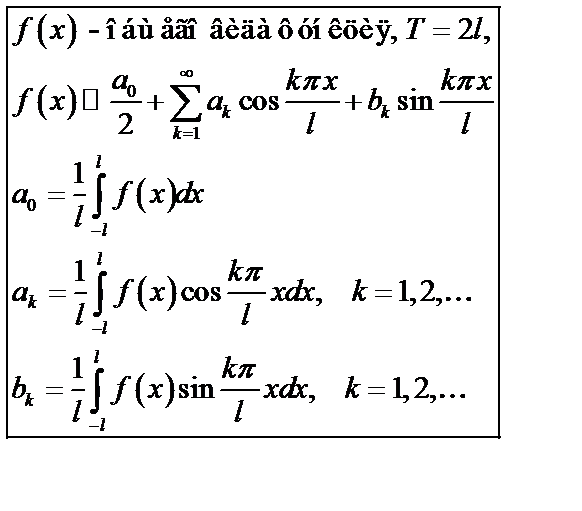
Частный случай: .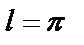

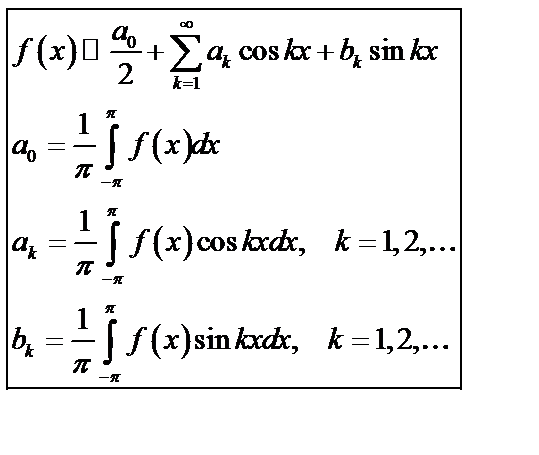
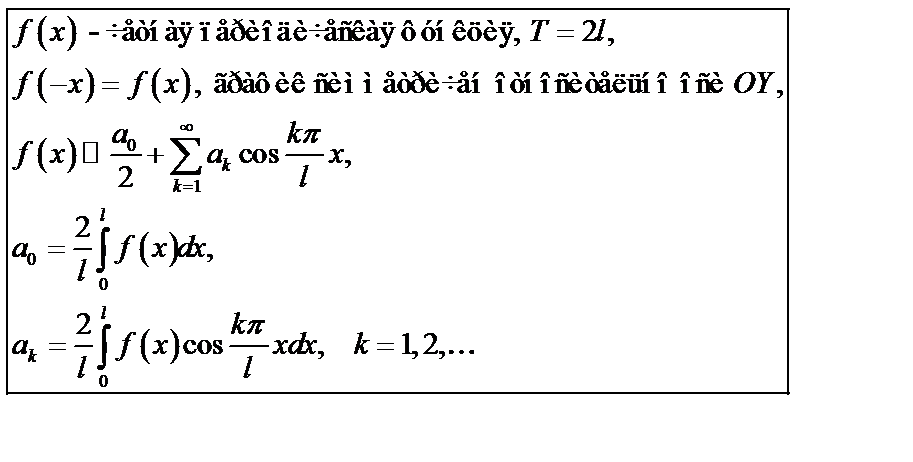(50)

Частный случай: .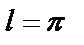

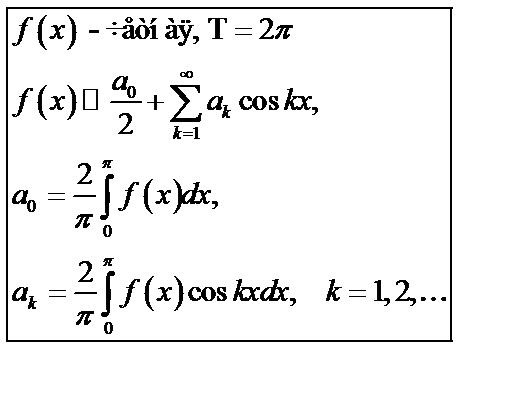
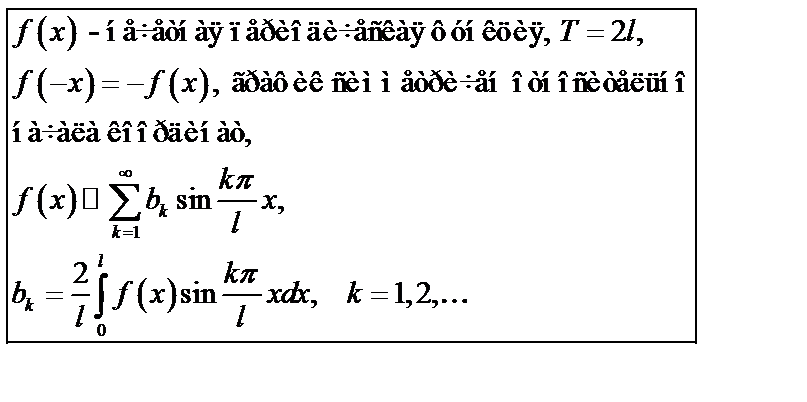
Частный случай: .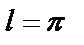

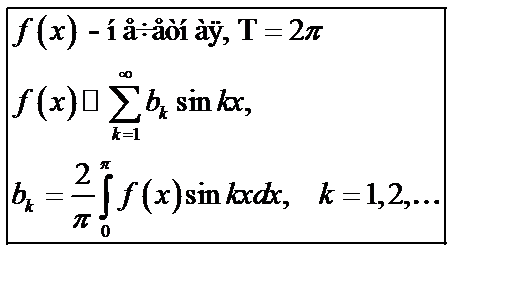(51)

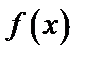– периодическая функция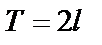

Пример. Разложить в ряд Фурье периодическую функцию с периодом 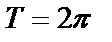, определенную на 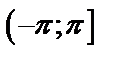следующим образом: .

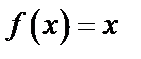Решение: Построим график функции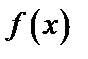

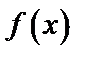
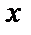
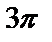
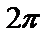
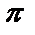
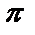
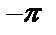
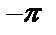
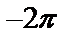
Рис. 11

Очевидно, что функция 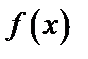на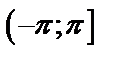

а) кусочно-непрерывна (имеет одну точку разрыва 1 рода, );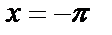

б) монотонна (возрастает) на 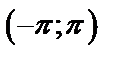, т.е. удовлетворяет условиям Дирихле. Запишем для нее ряд Фурье (формулы 51)

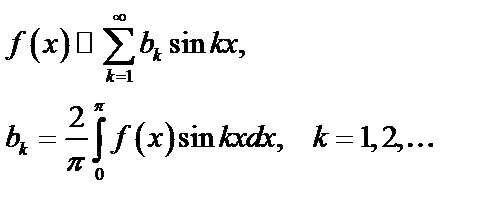
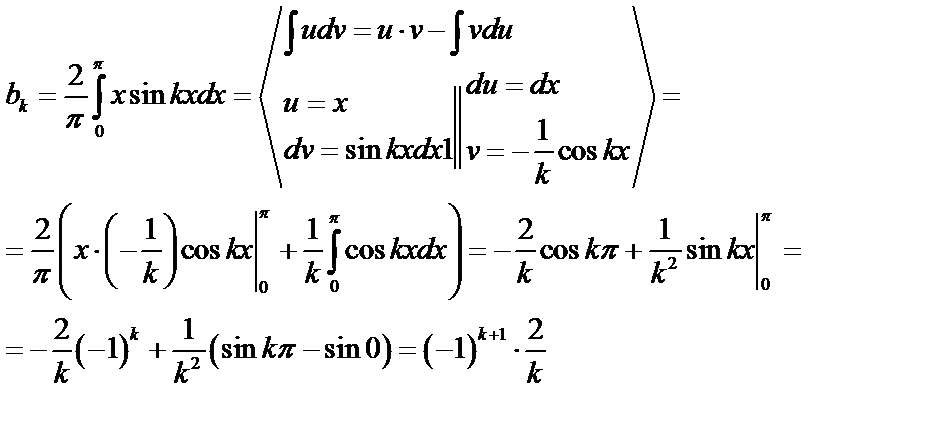
Таким образом,

.

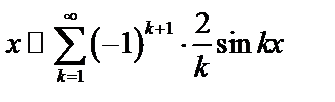При этом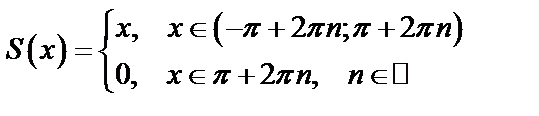

График :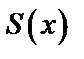

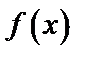
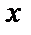
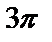
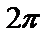
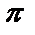
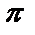
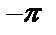
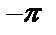
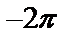
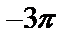
Рис. 12