2015-05-13
401
Дан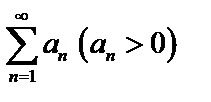 
, члены которого не возрастают. Если существует функция 
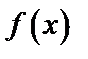, которая определена при всех 
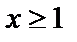, непрерывна, не возрастает и 
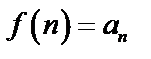, тогда 
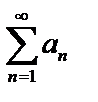сходится или расходится одновременно с несобственным интегралом 
.
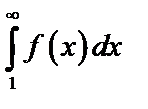Пример. Исследовать на сходимость ряд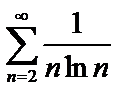 
.
Решение: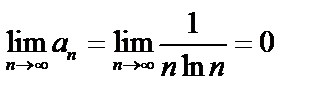 
, отсюда ничего про сходимость, расходимость ряда сказать нельзя. Ряд знакоположительный, применим к нему интегральный признак сходимости.
Рассмотрим функцию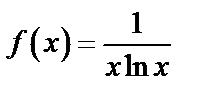 
при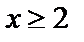 
, эта функция непрерывна, убывает и 
.
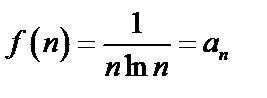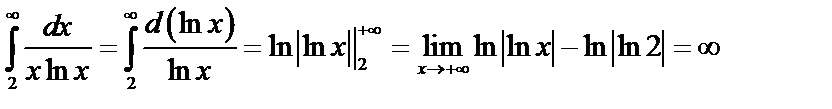, т.е. интеграл расходится, а значит и ряд расходится.
