Скалярным полем называют часть пространства, каждой точке 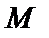 которого ставится в соответствие скалярная величина
которого ставится в соответствие скалярная величина 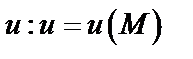 .
.
В декартовой системе 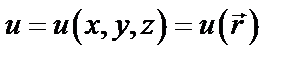 , где
, где 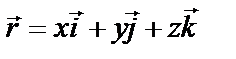 – радиус-вектор точки
– радиус-вектор точки  . Скалярные поля можно изучать с помощью поверхностей уровня, на которых
. Скалярные поля можно изучать с помощью поверхностей уровня, на которых 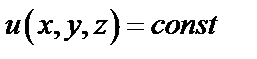 . Для плоского скалярно поля рассматривают линии уровня, их уравнение
. Для плоского скалярно поля рассматривают линии уровня, их уравнение 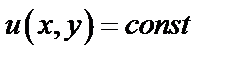 .
.
Производной скалярного поля по данному направлению 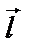 называют предел отношения приращения поля (функции) в данной точке
называют предел отношения приращения поля (функции) в данной точке 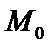 и данном направлении к длине направляющего вектора, при условии, что
и данном направлении к длине направляющего вектора, при условии, что 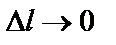
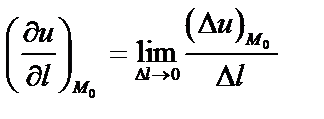 ,
,
Если направляющие косинусы 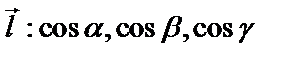 , то в координатной форме
, то в координатной форме 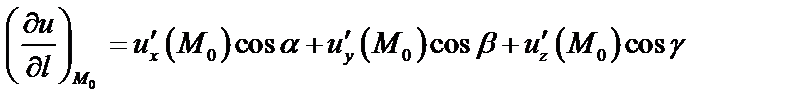 .
.
Градиент скалярного поля в данной точке – это вектор, направленный в сторону наибольшего возрастания поля.
В координатной форме: 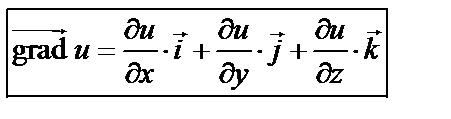 . (52)
. (52)
Между производной по направлению и градиентом существует связь:
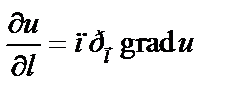 .
.
 2015-05-13
2015-05-13 2962
2962
