Числовые характеристики случайной величины

Математическим ожиданием Д.С.В. 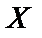называют сумму произведений всех ее возможных значений 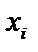на соответствующие вероятности :

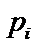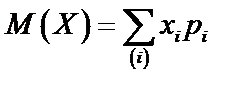(65)

Математическим ожиданием Н.С.В. 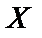с плотностью 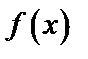называют ее среднее значение, вычисляемое по формуле

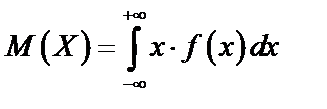
Математическое ожидание случайной величины может и не существовать, если соответствующая сумма или интеграл расходятся.

Обозначают .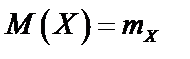

Свойства :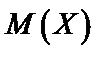

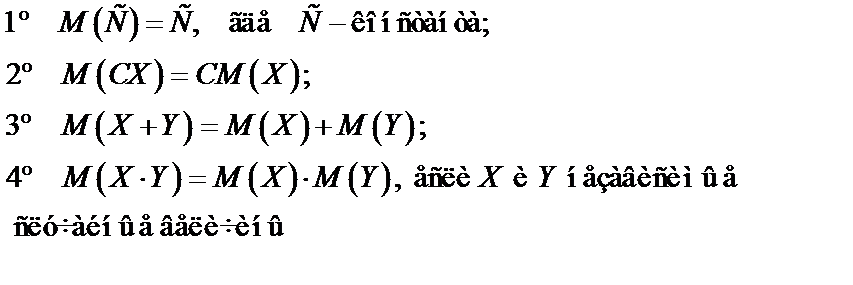
Центрированной случайной величиной 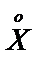называют разность между случайной величиной 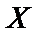и ее математическим ожиданием:

.

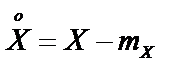Дисперсией случайной величины 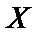называют математическое ожидание квадрата соответствующей центрированной случайной величины:

.

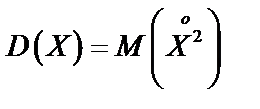Для Д.С.В. дисперсия вычисляется по формуле:

,

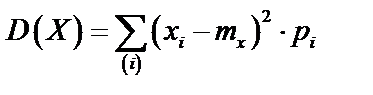для Н.С.В.:

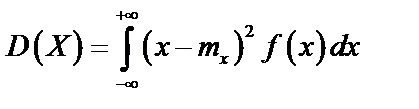
Свойства дисперсии:

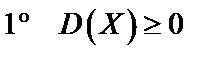, причем 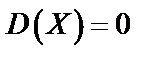, если 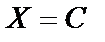, где 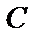– константа;

;

;

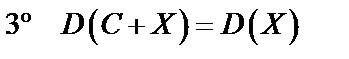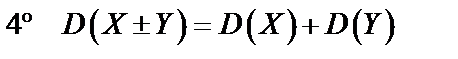, есл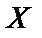и и 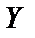– независимые случайные величины,

,

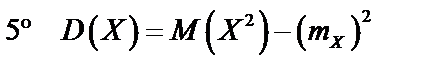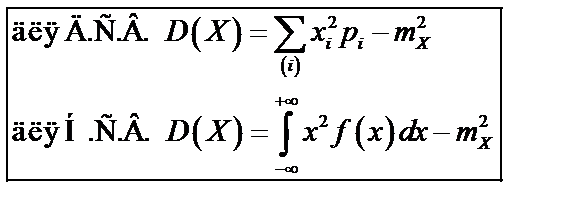. (66)

Корень квадратный из дисперсии называют средним квадратичным отклонением (стандартным отклонением) и обозначают через 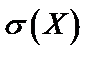или :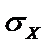

.

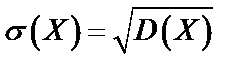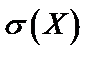есть характеристика рассеивания, разбросанности случайной величины около ее математического ожидания, само слово «дисперсия» означает «рассеивание».