


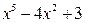
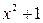

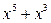
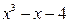

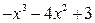

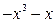
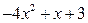

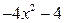
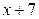


 Следовательно,
Следовательно, 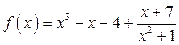 .
.
Правильные рациональные дроби вида
І. 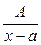 ,
,
ІІ. 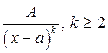 ,
,
ІІІ. 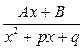 ,
,
IV. 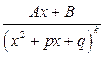 ,
, 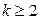 ,
,
где 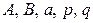 – действительные числа,
– действительные числа, 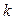 - натуральное число, а трехчлен
- натуральное число, а трехчлен 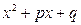 имеет комплексные корни
имеет комплексные корни 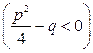 , называются простейшими дробями І, ІІ, ІІІ и IV типов.
, называются простейшими дробями І, ІІ, ІІІ и IV типов.
Справедливо следующее утверждение: правильная несократимая рациональная дробь 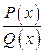 , знаменатель которой
, знаменатель которой
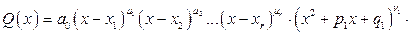
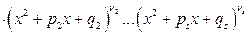 , может быть единственным образом разложена в сумму простейших дробей.
, может быть единственным образом разложена в сумму простейших дробей.
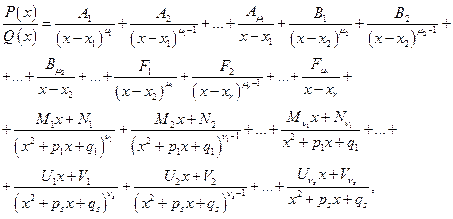
где 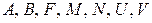 (с соответствующими индексами) – некоторые постоянные.
(с соответствующими индексами) – некоторые постоянные.
Указанные постоянные могут быть найдены методом неопределенных коэффициентов одним из трех способов:
1) способ сравнения коэффициентов при одинаковых степенях 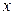 ;
;
2) способ подстановки частных значений 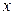 ;
;
3) комбинированный способ.
► Напишите разложение правильной несократимой дроби 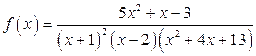 на простейшие, не вычисляя коэффициентов.
на простейшие, не вычисляя коэффициентов.
Пример 1.8. Представить в виде суммы простейших дробей дробно-рациональную функцию 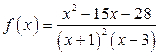 .
.
Решение. Заданная дробь правильная 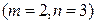 и несократимая, поскольку
и несократимая, поскольку 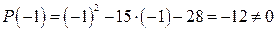 ,
, 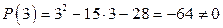 . Ее разложение в сумму простейших дробей имеет вид:
. Ее разложение в сумму простейших дробей имеет вид:
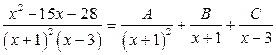 ,
,
где 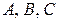 – неопределенные коэффициенты.
– неопределенные коэффициенты.
Приведем правую часть к общему знаменателю:
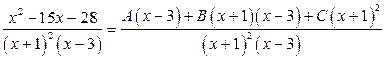 .
.
Поскольку дроби равны и имеют одинаковые знаменатели, то должны быть равны их числители:
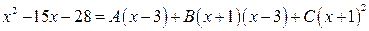 . (1.6)
. (1.6)
Воспользуемся сначала способом подстановки частных значений 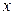 . Наиболее удобно брать значения корней знаменателя.
. Наиболее удобно брать значения корней знаменателя.
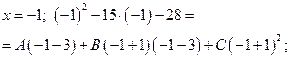
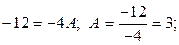
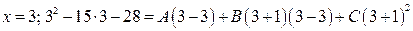
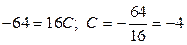 .
.
Поскольку других корней нет, то используем способ приравнивания коэффициентов при одинаковых степенях 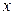 в левой и правой частях равенства (1.6).
в левой и правой частях равенства (1.6).
Для этого равенство (1.6) запишем в виде
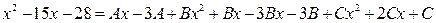
или
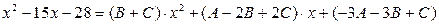 . (1.7)
. (1.7)
Приравнивая коэффициенты при 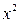 в равенстве (1.8), получаем
в равенстве (1.8), получаем
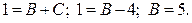
Учитывая полученные результаты, можем записать:
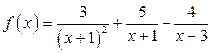 .
.
 2015-05-13
2015-05-13 488
488








