В разделе «Дифференциальное исчисление функций одной переменной» рассматривалась задача: по заданной функции найти ее производную. В данном разделе – «Интегральное исчисление функций одной переменной» решается обратная задача: известна производная функции  , а нужно найти саму функцию
, а нужно найти саму функцию  . Например, с механической точки зрения это означает, что по известной скорости движения материальной точки необходимо восстановить закон ее движения, т.е. зависимость пройденного пути от времени.
. Например, с механической точки зрения это означает, что по известной скорости движения материальной точки необходимо восстановить закон ее движения, т.е. зависимость пройденного пути от времени.
Во многих областях науки и техники приходится решать задачу восстановления функции по известной ее производной.
Функция 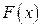 называется первообразной функцией для функции
называется первообразной функцией для функции  на интервале
на интервале 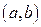 , если она дифференцируема на
, если она дифференцируема на 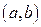 и
и 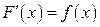 .
.
Например, для функции 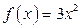 первообразной является функция
первообразной является функция 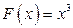 на
на 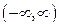 , поскольку
, поскольку 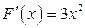 . Заметим, что первообразной для
. Заметим, что первообразной для 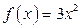 на
на 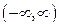 является также любая из функций
является также любая из функций 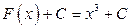 , где
, где 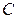 – любое число.
– любое число.
► Запишите первообразные для функций
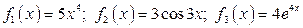 .
.
Справедливо следующее утверждение: если 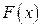 – первообразная для функции
– первообразная для функции  на
на 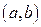 , то
, то 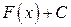 , где
, где 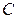 – произвольная постоянная, также первообразная для
– произвольная постоянная, также первообразная для  на
на 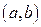 . Более того, любая другая первообразная имеет такой же вид.
. Более того, любая другая первообразная имеет такой же вид.
Совокупность всех первообразных для функции  на интервале
на интервале 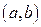 называется неопределенным интегралом от функции
называется неопределенным интегралом от функции  и обозначается символом
и обозначается символом 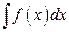 . Таким образом,
. Таким образом,
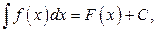 если
если 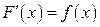 .
.
При этом функция  называется подынтегральной функцией,
называется подынтегральной функцией, 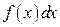 называется подынтегральным выражением.
называется подынтегральным выражением.
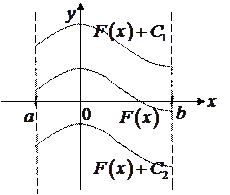
Рис. 2.1.
Нахождение первообразной для данной функции  называется интегрированием функции
называется интегрированием функции  . Если функция непрерывна на
. Если функция непрерывна на 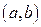 , то для нее существует первообразная на
, то для нее существует первообразная на 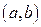 , а, следовательно, неопределенный интеграл, т.е. функция
, а, следовательно, неопределенный интеграл, т.е. функция  интегрируема на
интегрируема на 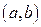 .
.
► Запишите определение первообразной и неопределенного интеграла.
► Всякая ли функция интегрируема на интервале 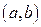 ?
?
Укажем ряд свойств неопределенного интеграла, вытекающих из его определения.
1. 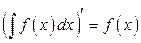 .
.
2. 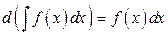 .
.
3. 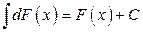 или
или 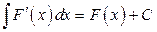 .
.
4. 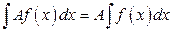 ,
, 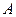 - постоянная величина.
- постоянная величина.
5. 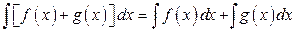 .
.
6. Если 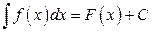 , то
, то
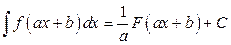 .
.
► Запишите словесные формулировки свойств 1-5 неопределенного интеграла.
Непосредственно из определения неопределенного интеграла и таблицы производных, приведенной в разделе «Дифференциальное исчисление функций одной переменной», вытекает таблица интегралов (справедливость написанных в ней равенств легко проверить применением первого свойства неопределенного интеграла):
1. 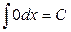 2. 2. 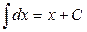 3. 3. 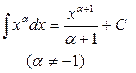 4. 4. 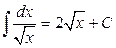 5. 5. 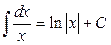 6. 6. 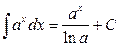 7. 7. 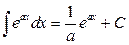 8. 8. 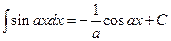 9. 9. 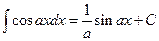 10. 10. 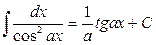 | 11. 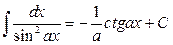 12. 12. 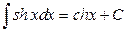 13. 13. 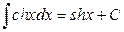 14. 14. 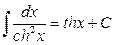 15. 15. 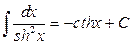 16 16 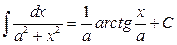 17. 17.  18. 18. 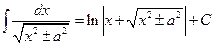 19. 19. 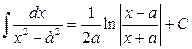 20. 20. 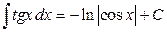 21 21 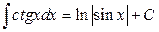 22. 22. 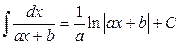 |
► Найти неопределенные интегралы:
1. 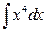 , 2.
, 2. 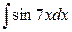 , 3.
, 3. 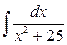 , 4.
, 4. 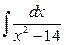 , 5.
, 5. 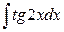 .
.
Отметим три основных метода нахождения неопределенного интеграла:
1) непосредственное интегрирование;
2) метод замены переменной (метод подстановки);
3) метод интегрирования по частям.
Непосредственное интегрирование.
Непосредственное интегрирование – это нахождение неопределенного интеграла путем использования его основных свойств и таблицы интегралов.
Пример 2.1. Найти неопределенные интегралы и проверить правильность полученных результатов.
1. 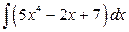 ; 2.
; 2. 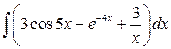 .
.
Решение. Для нахождения заданных интегралов используем свойство 5), а затем 4) неопределенных интегралов: неопределенный интеграл от суммы нескольких функций равен сумме неопределенных интегралов от этих функций и постоянный множитель можно выносить за знак неопределенного интеграла.
1) 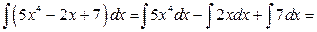
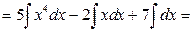
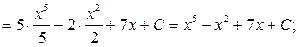
2) 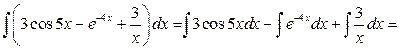
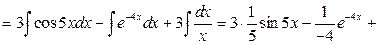
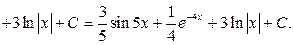
Проверка. В соответствии со свойством 1) неопределенного интеграла производная от полученного результата должна совпадать с подинтегральной функцией.
1) 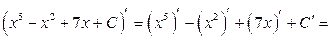
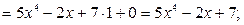
2) 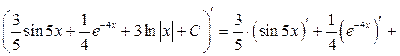
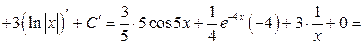
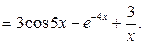
В обоих случаях результат дифференцирования совпадает с подынтегральной функцией, следовательно, интегралы найдены верно.
▶ Найти неопределенные интегралы. Проверить правильность полученных результатов.
а) 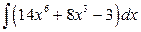 , б)
, б) 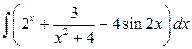 ,
,
в) 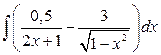 .
.
Ответ: 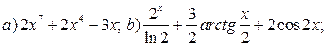
 2015-05-13
2015-05-13 2232
2232
