Метод замены переменной (метод подстановки)

Как указано во втором разделе метод замены переменной наиболее используемый метод, который часто применяется предварительно даже тогда, когда используется другой метод, например, интегрирование по частям или интегрирование рациональных дробей.

► Опишите метод замены переменной для неопределенного интеграла.

Применение метода подстановки в определенном интеграле базируется на следующем утверждении:

пусть задан 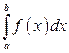, в котором функция непрерывна на отрезке 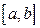. Введем новую переменную 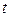по формуле .

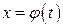Если

1) ;

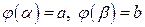2) функци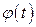и и 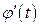непрерывны на отрезке ;

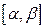3) 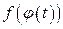определена и непрерывна на отрезке 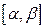, то

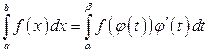. (3.4)

Отметим, что при вычислении определенного интеграла методом подстановки следует обязательно пересчитать пределы интегрирования и, благодаря этому, в конечном результате нет необходимости возвращаться к исходной переменной, как это делается в неопределенном интеграле.

Пример 3.2. Вычислить 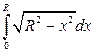, применив метод замены переменной.