Пусть 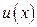 и
и 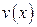 - непрерывно дифференцируемые на
- непрерывно дифференцируемые на 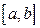 функции. Справедлива формула интегрирования по частям для определенного интеграла
функции. Справедлива формула интегрирования по частям для определенного интеграла
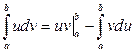
Отметим: все, что указывалось во втором разделе по поводу типа функций, неопределенные интегралы от которых находятся методом интегрирования по частям, полностью справедливо и для определенного интеграла.
► Укажите в приведенных ниже определенных интегралах, что следует принять в качестве 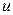 , а что в качестве
, а что в качестве 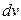 при применении метода интегрирования по частям.
при применении метода интегрирования по частям.
1) 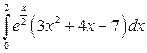 ; 2)
; 2) 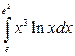 ;
;
3) 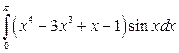 ; 4)
; 4) 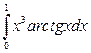 .
.
Пример 3.3. Вычислить определенные интегралы, применяя метод интегрирования по частям.
1) 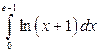 ; 2)
; 2) 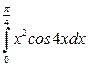 .
.
Решение.
1) 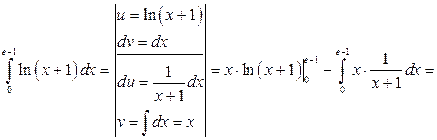
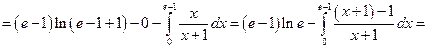
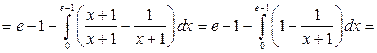
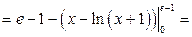
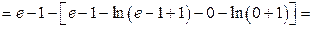
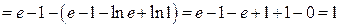 .
.
Напомним, что 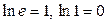 .
.
2) 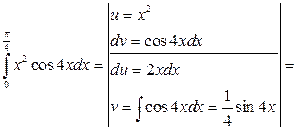
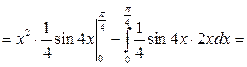
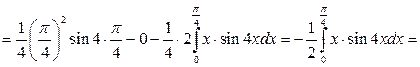
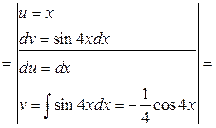
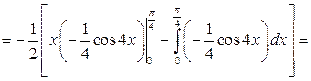
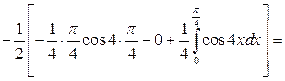
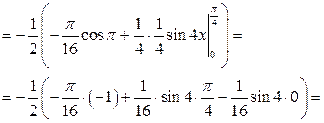
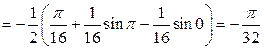 ,
,
учтено, что 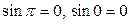 .
.
 2015-05-13
2015-05-13 403
403








