- Интегралы с бесконечными пределами.
Пусть функция  определена и непрерывна при всех значениях
определена и непрерывна при всех значениях 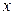 таких, что
таких, что 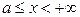 . Рассмотрим
. Рассмотрим 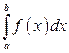 , который имеет смысл при любом значении
, который имеет смысл при любом значении 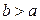 и меняется при изменении
и меняется при изменении 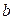 , т.е. является функцией от
, т.е. является функцией от 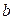 .
.
Если существует конечный предел
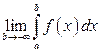 ,
,
то этот предел называют несобственным интегралом от функции  на промежутке
на промежутке 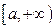 и обозначают символом
и обозначают символом 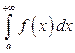 .
.
Таким образом, по определению
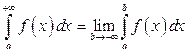 . (3.5)
. (3.5)
В этом случае говорят, что несобственный интеграл сходится. Если же в (3.5) предел не существует или равен бесконечности, то говорят, что 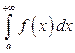 расходится.
расходится.
Несобственный интеграл 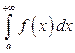 при
при 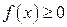 на промежутке
на промежутке 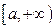 имеет следующий геометрический смысл: если
имеет следующий геометрический смысл: если 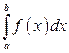 определяет площадь области, ограниченной кривой
определяет площадь области, ограниченной кривой 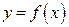 , осью абсцисс и прямыми
, осью абсцисс и прямыми 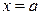 и
и 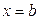 , то считают, что
, то считают, что 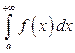 определяет площадь неограниченной (бесконечной) области, заключенной между линиями
определяет площадь неограниченной (бесконечной) области, заключенной между линиями 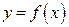 ,
, 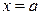 и осью абсцисс (рис.3.9).
и осью абсцисс (рис.3.9).
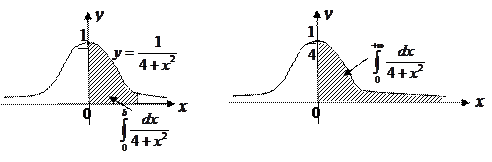
Рис.3.9.
Аналогично определяются несобственные интегралы и для других бесконечных промежутков.
По определению
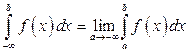
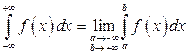 .
.
Определение сходимости, расходимости для этих интегралов такое же, как и для интеграла (3.5).
|
|
|
Пример 3.4. Исследовать на сходимость несобственный интеграл.
а) 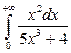 ; б)
; б) 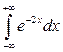 .
.
 2015-05-13
2015-05-13 322
322








