I. Решить уравнение. Сделать проверку. Изобразить корни уравнения на комплексной плоскости.
1. 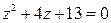 3.
3. 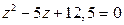 5.
5. 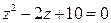 7.
7. 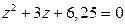 9.
9. 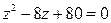 11.
11. 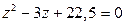 13.
13. 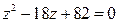 15.
15. 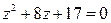 17.
17. 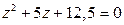 19.
19. 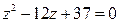 21.
21. 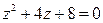 23.
23. 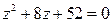 25.
25. 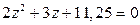 27.
27. 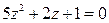 29.
29. 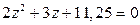
| 2. 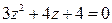 4.
4. 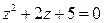 6.
6. 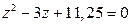 8.
8. 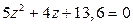 10.
10. 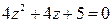 12.
12. 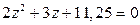 14.
14. 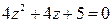 16.
16. 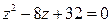 18.
18. 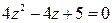 20.
20. 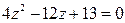 22.
22. 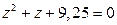 24.
24. 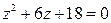 26.
26. 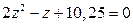 28.
28. 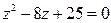 30.
30. 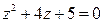
|
II. Даны числа 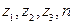 . Найти:
. Найти:
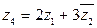 ;
; 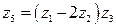 ;
; 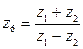 ;
; 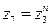 .
.
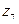 найти, используя тригонометрическую и показательную формы числа
найти, используя тригонометрическую и показательную формы числа 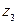 .
.
1. 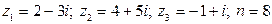 .
.
2. 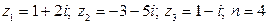 .
.
3. 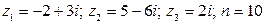 .
.
4. 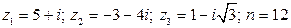
5. 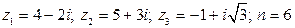 .
.
6. 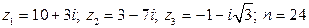 .
.
7. 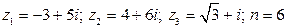 .
.
8. 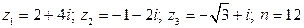 .
.
9. 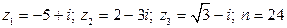 .
.
10. 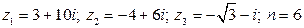 .
.
11. 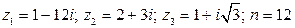 .
.
12. 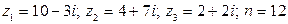 .
.
13. 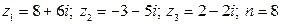 .
.
14. 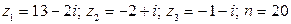 .
.
15. 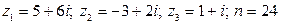 .
.
16. 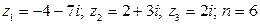 .
.
17. 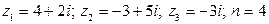 .
.
18. 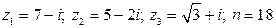 .
.
19. 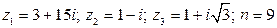 .
.
20. 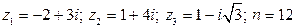 .
.
21. 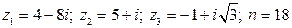 .
.
22. 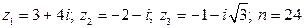 .
.
23. 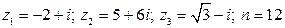 .
.
24. 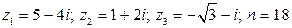
25. 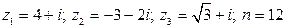
26. 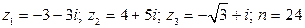 .
.
27. 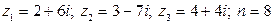 .
.
28. 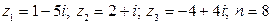 .
.
29. 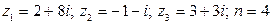 .
.
30. 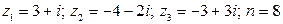 .
.
III. Решить уравнение, считая 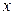 и
и 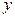 действительными числами. Сделать проверку.
действительными числами. Сделать проверку.
1. 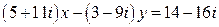 .
.
2. 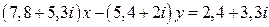 .
.
3. 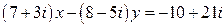 .
.
4. 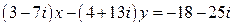
5. 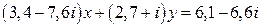 .
.
6. 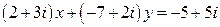 .
.
7. 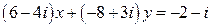 .
.
8. 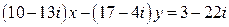 .
.
9. 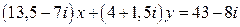 .
.
10. 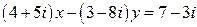 .
.
11. 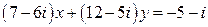 .
.
12. 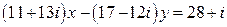 .
.
13. 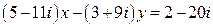 .
.
14. 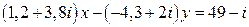 .
.
15. 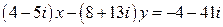 .
.
16. 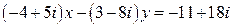 .
.
17. 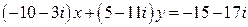 .
.
18. 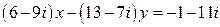 .
.
19. 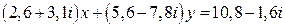 .
.
20. 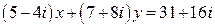 .
.
21. 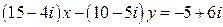 .
.
22. 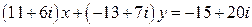
23. 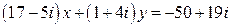 .
.
24. 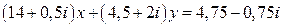 .
.
25. 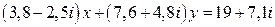 .
.
26. 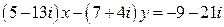 .
.
27. 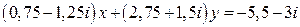 .
.
28. 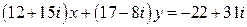 .
.
29. 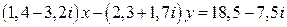 .
.
30.  .
.
IV. Разложить многочлен на простейшие множители с действительными коэффициентами.
1. а) 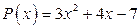 ; б)
; б) 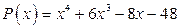 .
.
2. а) 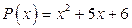 ; б)
; б) 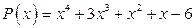 .
.
3. а) 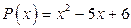 ; б)
; б) 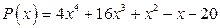 .
.
4. а) 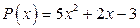 ; б)
; б) 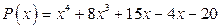 .
.
5. а) 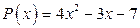 ; б)
; б) 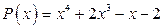 .
.
6. а) 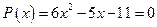 ; б)
; б) 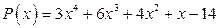 .
.
7. а) 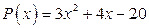 ; б)
; б) 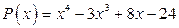 .
.
8. а) 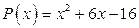 ; б)
; б) 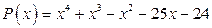 .
.
9. а) 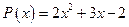 ; б)
; б) 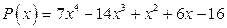 .
.
10. а) 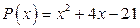 ; б)
; б) 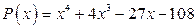 .
.
11. а) 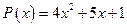 ; б)
; б) 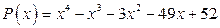 .
.
12. а) 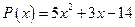 ; б)
; б) 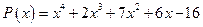 .
.
13. а) 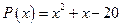 ; б)
; б) 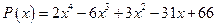 .
.
14. а) 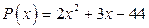 ; б)
; б) 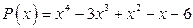 .
.
15. а) 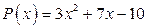 ; б)
; б) 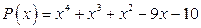 .
.
16. а) 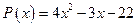 ; б)
; б) 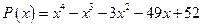 .
.
17. а) 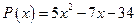 ; б)
; б) 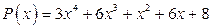 .
.
18. а) 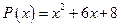 ; б)
; б) 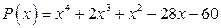 .
.
19. а) 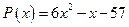 ; б)
; б) 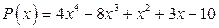 .
.
20. а) 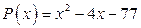 ; б)
; б) 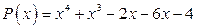 .
.
21. а) 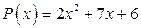 ; б)
; б) 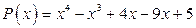 .
.
22. а) 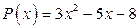 ; б)
; б) 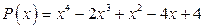 .
.
23. а) 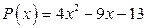 ; б)
; б) 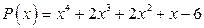 .
.
24. а) 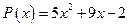 ; б)
; б) 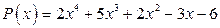 .
.
25. а) 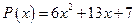 ; б)
; б) 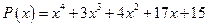 .
.
26. а) 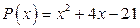 ; б)
; б) 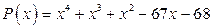 .
.
27. а) 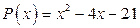 ; б)
; б) 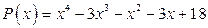 .
.
28. а) 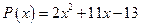 ; б)
; б) 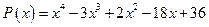 .
.
29. а) 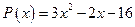 ; б)
; б) 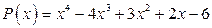 .
.
30. а) 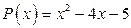 ; б)
; б) 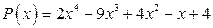 .
.
V. Найти неопределенные интегралы.
В каждом случае записать табличный интеграл и значения входящих в него параметров.
1. 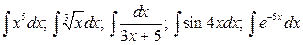 .
.
2. 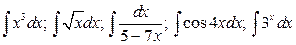 .
.
3. 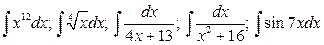 .
.
4. 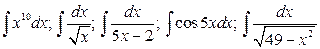 .
.
5. 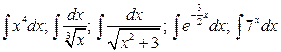 .
.
6. 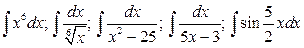 .
.
7. 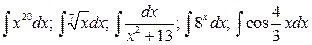 .
.
8. 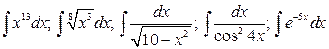
9. 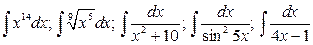 .
.
10. 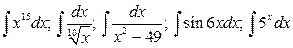 .
.
11. 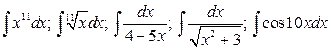 .
.
12. 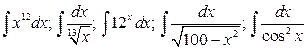 .
.
13. 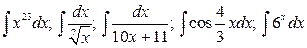 .
.
14. 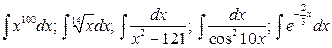 .
.
15. 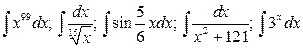 .
.
16. 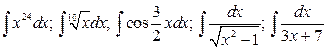 .
.
17. 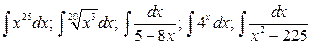 .
.
18. 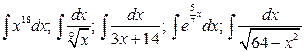 .
.
19. 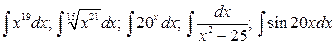 .
.
20. 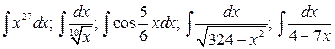 .
.
21. 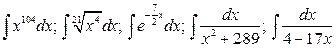 .
.
22. 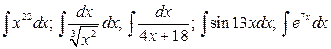 .
.
23. 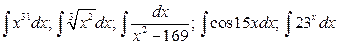 .
.
24. 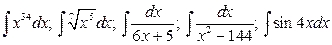 .
.
25. 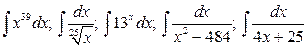 .
.
26. 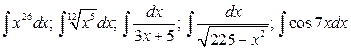 .
.
27. 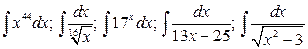 .
.
28. 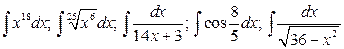 .
.
29. 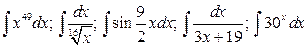 .
.
30. 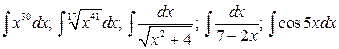 .
.
VI. Найти неопределенные интегралы, пользуясь методом подстановки или применяя интегрирование по частям.
1. а) 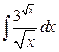 ; б)
; б) 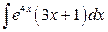 .
.
2. а) 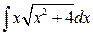 ; б)
; б) 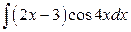 .
.
3. а) 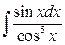 ; б)
; б) 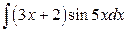 .
.
4. а) 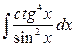 ; б)
; б) 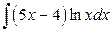 .
.
5. а) 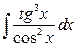 ; б)
; б) 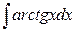 .
.
6. а) 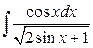 ; б)
; б) 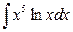 .
.
7. а) 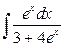 ; б)
; б) 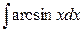 .
.
8. а) 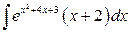 ; б)
; б) 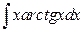 .
.
9. а) 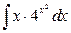 ; б)
; б) 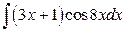 .
.
10. а) 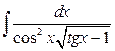 ; б)
; б) 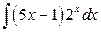 .
.
11. а) 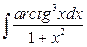 ; б)
; б) 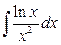 .
.
12. а) 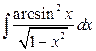 ; б)
; б) 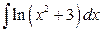 .
.
13. а) 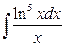 ; б)
; б) 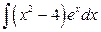 .
.
14. а) 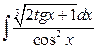 ; б)
; б) 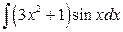 .
.
15. а) 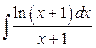 ; б)
; б) 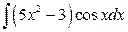 .
.
16. а) 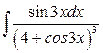 ; б)
; б) 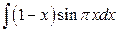 .
.
17. а) 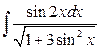 ; б)
; б) 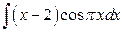 .
.
18. а) 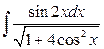 ; б)
; б) 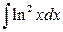 .
.
19. а) 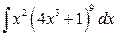 ; б)
; б) 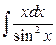 .
.
20. а) 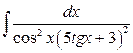 ; б)
; б) 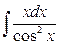 .
.
21. а) 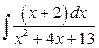 ; б)
; б) 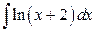 .
.
22. а) 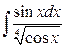 ; б)
; б) 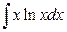 .
.
23. а) 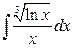 ; б)
; б) 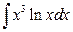 .
.
24. а) 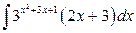 ; б)
; б) 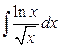 .
.
25. а) 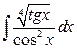 ; б)
; б) 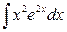 .
.
26. а) 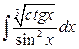 ; б)
; б) 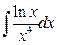 .
.
27. а) 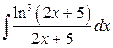 ; б)
; б) 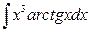 .
.
28. а) 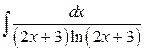 ; б)
; б) 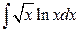 .
.
29. а) 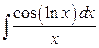 ; б)
; б) 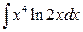 .
.
30. а) 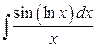 ; б)
; б) 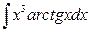 .
.
VII. Найти интегралы от рациональных дробей.
1. а) 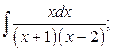 б)
б) 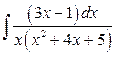 .
.
2. а) 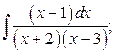 б)
б) 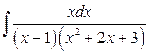 .
.
3. а) 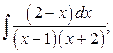 б)
б) 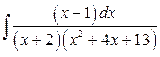 .
.
4. а) 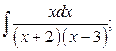 б)
б) 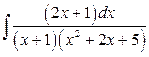 .
.
5. а) 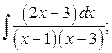 б)
б) 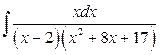 .
.
6. а) 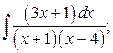 б)
б) 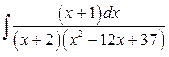 .
.
7. а) 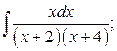 б)
б) 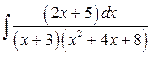 .
.
8. а) 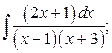 б)
б) 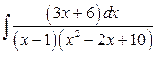 .
.
9. а) 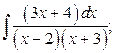 б)
б) 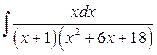 .
.
10. а) 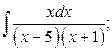 б)
б) 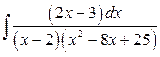 .
.
11. а) 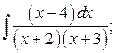 б)
б) 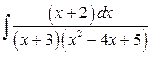 .
.
12. а) 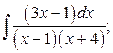 б)
б) 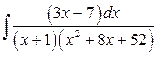 .
.
13. а) 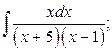 б)
б) 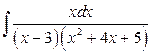 .
.
14. а) 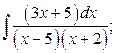 б)
б) 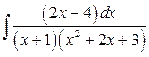 .
.
15. а) 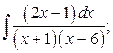 б)
б) 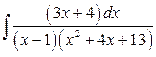 .
.
16. а) 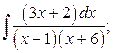 б)
б) 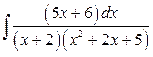 .
.
17. а) 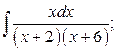 б)
б) 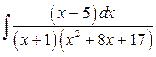 .
.
18. а)  б)
б) 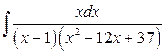 .
.
19. а) 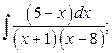 б)
б) 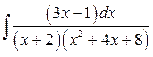 .
.
20. а) 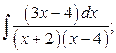 б)
б) 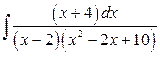 .
.
21. а) 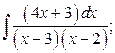 б)
б) 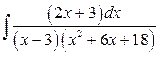 .
.
22. а) 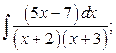 б)
б) 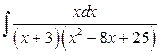 .
.
23. а) 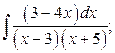 б)
б) 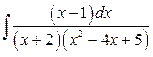 .
.
24. а) 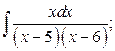 б)
б) 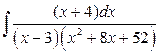 .
.
25. а) 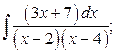 б)
б) 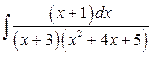 .
.
26. а) 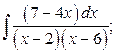 б)
б) 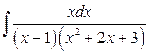 .
.
27. а) 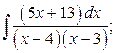 б)
б) 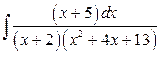 .
.
28. а) 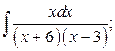 б)
б) 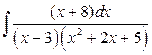 .
.
29. а) 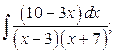 б)
б) 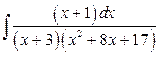 .
.
30. а) 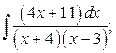 б)
б) 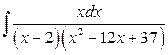 .
.
VIII. Найти неопределенные интегралы от выражений, содержащих тригонометрические функции.
1. а) 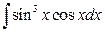 ; б)
; б) 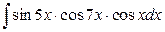 .
.
2. а) 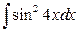 ; б)
; б) 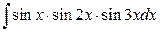 .
.
3. а) 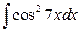 ; б)
; б) 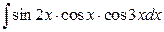 .
.
4. а) 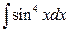 ; б)
; б) 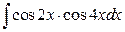 .
.
5. а) 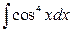 ; б)
; б) 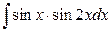 .
.
6. а) 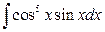 ; б)
; б) 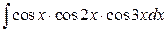 .
.
7. а) 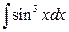 ; б)
; б) 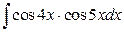 .
.
8. а) 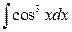 ; б)
; б) 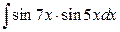 .
.
9. а) 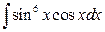 ; б)
; б) 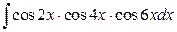 .
.
10. а) 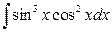 ; б)
; б) 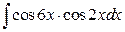 .
.
11. а) 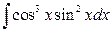 ; б)
; б) 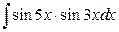 .
.
12. а) 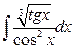 ; б)
; б) 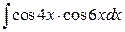 .
.
13. а) 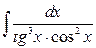 ; б)
; б) 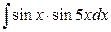 .
.
14. а) 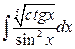 ; б)
; б) 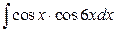 .
.
15. а) 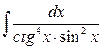 ; б)
; б) 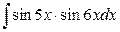 .
.
16. а) 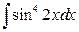 ; б)
; б) 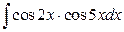 .
.
17. а) 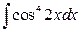 ; б)
; б) 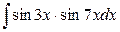 .
.
18. а) 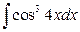 ; б)
; б) 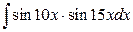 .
.
19. а) 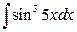 ; б)
; б) 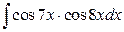 .
.
20. а) 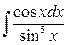 ; б)
; б) 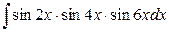 .
.
21. а) 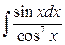 ; б)
; б) 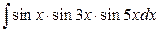 .
.
22. а) 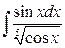 ; б)
; б) 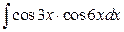 .
.
23. а) 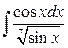 ; б)
; б) 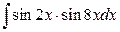 .
.
24. а) 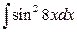 ; б)
; б) 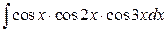 .
.
25. а) 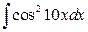 ; б)
; б) 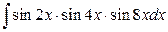 .
.
26. а) 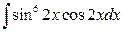 ; б)
; б) 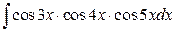 .
.
27. а) 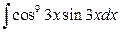 ; б)
; б) 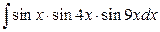 .
.
28. а) 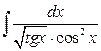 ; б)
; б) 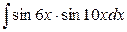 .
.
29. а) 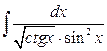 ; б)
; б) 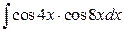 .
.
30. а) 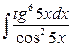 ; б)
; б) 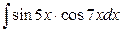 .
.
IX. Вычислить определенные интегралы.
1. а) 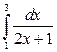 ; б)
; б) 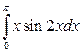 ; в)
; в) 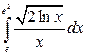 .
.
2. а) 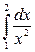 ; б)
; б) 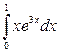 ; в)
; в) 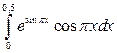 .
.
3. а) 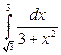 ; б)
; б) 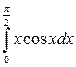 ; в)
; в) 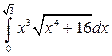 .
.
4. а) 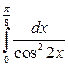 ; б)
; б) 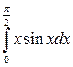 ; в)
; в) 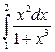 .
.
5. а) 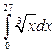 ; б)
; б) 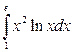 ; в)
; в) 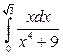 .
.
6. а) 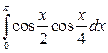 ; б)
; б) 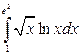 ; в)
; в) 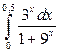 .
.
7. а) 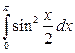 ; б)
; б) 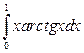 ; в)
; в) 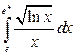 .
.
8. а) 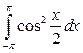 ; б)
; б) 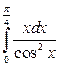 ; в)
; в) 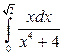 .
.
9. а) 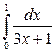 ; б)
; б) 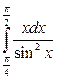 ; в)
; в) 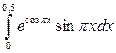 .
.
10. а) 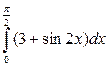 ; б)
; б) 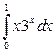 ; в)
; в) 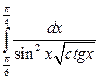 .
.
11. а) 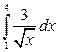 ; б)
; б) 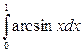 ; в)
; в) 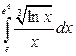 .
.
12. а) 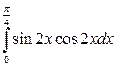 ; б)
; б) 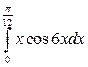 ; в)
; в) 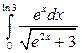 .
.
13. а) 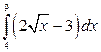 ; б)
; б) 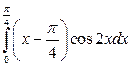 ; в)
; в) 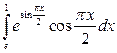 .
.
14. а) 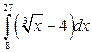 ; б)
; б) 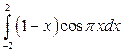 ; в)
; в) 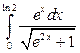 .
.
15. а) 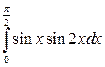 ; б)
; б) 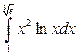 ; в)
; в) 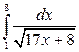 .
.
16. а) 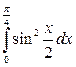 ; б)
; б) 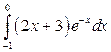 ; в)
; в) 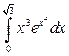 .
.
17. а) 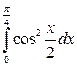 ; б)
; б) 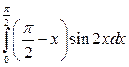 ; в)
; в) 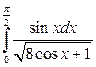 .
.
18. а) 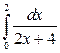 ; б)
; б) 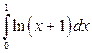 ; в)
; в) 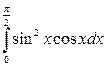 .
.
19. а) 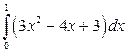 ; б)
; б) 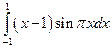 ; в)
; в) 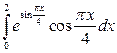 .
.
20. а) 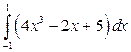 ; б)
; б) 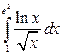 ; в)
; в) 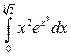 .
.
21. а) 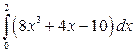 ; б)
; б) 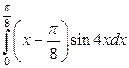 ; в)
; в) 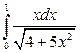 .
.
22. а) 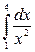 ; б)
; б) 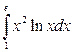 ; в)
; в) 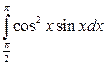 .
.
23. а) 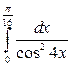 ; б)
; б) 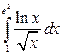 ; в)
; в) 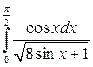 .
.
24. а) 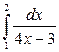 ; б)
; б) 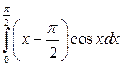 ; в)
; в) 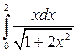 .
.
25. а) 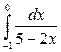 ; б)
; б) 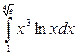 ; в)
; в) 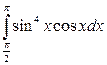 .
.
26. а) 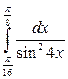 ; б)
; б) 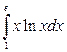 ; в)
; в) 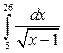 .
.
27. а) 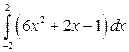 ; б)
; б) 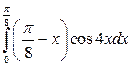 ; в)
; в) 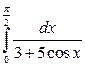 .
.
28. а) 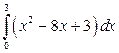 ; б)
; б) 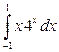 ; в)
; в) 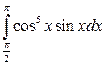 .
.
29. а) 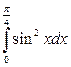 ; б)
; б) 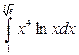 ; в)
; в) 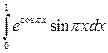 .
.
30. а) 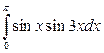 ; б)
; б) 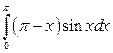 ; в)
; в) 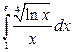 .
.
X. Вычислить:
- площадь фигуры, ограниченной параболой 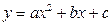 и прямой
и прямой 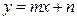 ;
;
- объем тела, образованного вращением вокруг оси 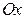 фигуры, ограниченной параболой
фигуры, ограниченной параболой 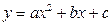 и прямой
и прямой 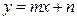 (значения параметров
(значения параметров 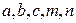 приведены в таблице).
приведены в таблице).
| № варианта | 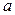
| 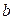
| 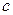
| 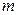
| 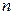
|
| -1 | |||||
| -4 | -2 | ||||
| -2 | -3 | ||||
| -4 | -2 | ||||
| -5 | -4 | ||||
| -4 | -3 | ||||
| -1 | |||||
| -3 | |||||
| -5 | -1 | ||||
| -2 | |||||
| -4 | -3 | ||||
| -5 | -3 | ||||
| -4 | |||||
| -3 | |||||
| -4 | |||||
| -1 | |||||
 2015-05-13
2015-05-13 488
488







