а) 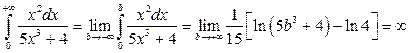 .
.
Следовательно, интеграл расходится.
Вспомогательные вычисления.
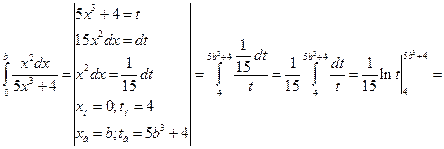
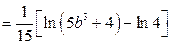 ;
;
б) 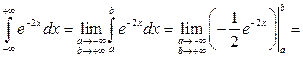
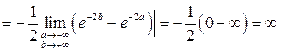 .
.
Интеграл расходится.
▶ Исследовать сходимость несобственных интегралов.
а) 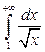 ; б)
; б) 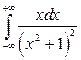 ; в)
; в) 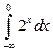 .
.
Ответы: а) расходится; б) сходится; в) сходится.
2. Интегралы от неограниченных функций.
Рассмотрим функцию  , заданную на отрезке
, заданную на отрезке 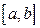 и такую, что она ограничена и интегрируема на каждом промежутке
и такую, что она ограничена и интегрируема на каждом промежутке 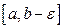 и неограниченна на отрезке
и неограниченна на отрезке 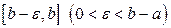 . Точку
. Точку 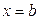 в этом случае называют особой точкой функции
в этом случае называют особой точкой функции  .
.
По определению
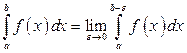 (особая точка
(особая точка 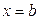 ). (3.6)
). (3.6)
Если предел в равенстве (3.6) существует и конечен, то говорят, что несобственный интеграл сходится, а функция  называется интегрируемой на отрезке
называется интегрируемой на отрезке 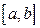 .
.
Если же предел бесконечен или не существует, то говорят, что интеграл расходится.
Аналогично определяется несобственный интеграл от неограниченной функции  , если особой точкой является нижний предел интегрирования
, если особой точкой является нижний предел интегрирования 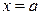 или точка
или точка 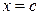 , лежащая внутри отрезка
, лежащая внутри отрезка 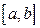
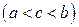 :
:
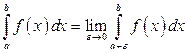 (особая точка
(особая точка 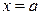 );
);
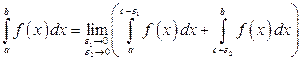 (особая точка
(особая точка 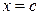 ).
).
Сходимость и расходимость этих несобственных интегралов определяется так же, как и для интеграла (3.6).
► Запишите определение несобственного интеграла с бесконечными пределами и несобственного интеграла от неограниченной функции.
► В каком случае несобственный интеграл называется сходящимся?
Пример 3.5. Исследовать сходимость несобственных интегралов.
а) 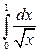 ; б)
; б) 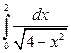 .
.
 2015-05-13
2015-05-13 384
384








