Цель работы – измерение моментов инерции твердых тел при помощи крутильных колебаний.
Лабораторная установка, входящая в состав комплекса «Физические основы механики», состоит из электронного блока (2) для измерения времени движения и числа 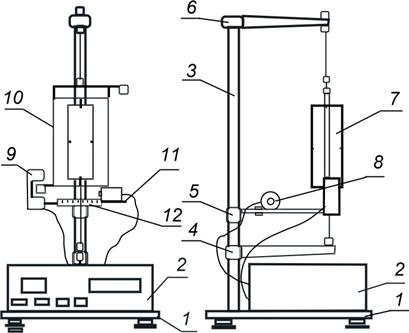 периодов, установленного на основании (1). На вертикальной колонне (3) закреплены три кронштейна: нижний (4), средний (5) и верхний (6). Между верхним и нижним кронштейнами натянута проволока, удерживающая рамку (10). На среднем кронштейне держится подковообразная стальная плита (11), которая служит основанием фотоэлектрическому датчику (9), электромагниту (8) и шкалой для измерения угла отклонения (12).
периодов, установленного на основании (1). На вертикальной колонне (3) закреплены три кронштейна: нижний (4), средний (5) и верхний (6). Между верхним и нижним кронштейнами натянута проволока, удерживающая рамку (10). На среднем кронштейне держится подковообразная стальная плита (11), которая служит основанием фотоэлектрическому датчику (9), электромагниту (8) и шкалой для измерения угла отклонения (12).
Положение электромагнита можно менять. Верхнюю планку рамки можно перемещать и закреплять при помощи винтов и устанавливать в ней грузики различных форм и размеров (7).
Рис. 7. Установка «Крутильный маятник»
Показания миллисекундомера обнуляются при нажатии клавиши «СБРОС», после нажатия клавиши «ПУСК» отключается электромагнит и рамка приходит в движение. После нажатия кнопки «СТОП» время движения маятника измеряется до завершения очередного полного периода колебаний, то есть, до первого нечетного прохождения рамкой через фотодатчик.
Теория эксперимента: момент инерции твердого тела относительно произвольно направленной оси вращения, проходящей через центр масс, с единичным направляющим вектором 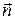 , имеющим координаты
, имеющим координаты 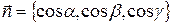 , вычисляется по формуле:
, вычисляется по формуле:
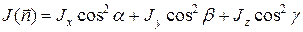 . (1)
. (1)
Здесь 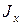 ,
, 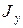 ,
, 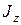 - компоненты тензора инерции в главных осях. В симметричных телах главные оси либо совпадают с осями симметрии, либо перпендикулярны плоскостям симметрии. В настоящей работе мы будем рассматривать куб и прямоугольные параллелепипеды. Система координат в главных осях в таких телах будет иметь начало в центе масс тела, а оси будут проходить перпендикулярно основным граням тел.
- компоненты тензора инерции в главных осях. В симметричных телах главные оси либо совпадают с осями симметрии, либо перпендикулярны плоскостям симметрии. В настоящей работе мы будем рассматривать куб и прямоугольные параллелепипеды. Система координат в главных осях в таких телах будет иметь начало в центе масс тела, а оси будут проходить перпендикулярно основным граням тел.
Для измерения моментов инерции тел будет использоваться метод крутильных колебаний. Твердое тело закрепляется в рамке крутильного маятника и под действием момента упругой силы возникающей в проволоке, рамка совершает крутильные колебания, уравнение которых имеет вид:
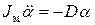 , (2)
, (2)
где 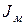 – момент инерции маятника с телом, D – постоянная момента упругих сил. Из уравнения (2) можно получить период крутильных колебаний:
– момент инерции маятника с телом, D – постоянная момента упругих сил. Из уравнения (2) можно получить период крутильных колебаний:
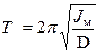 . (3)
. (3)
Момент инерции маятника складывается из момента инерции пустой рамки 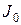 и момента инерции J закрепленного в ней тела:
и момента инерции J закрепленного в ней тела:
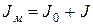 . (4)
. (4)
Очевидно, что период колебаний пустой рамки будет равен
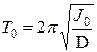 . (5)
. (5)
Из уравнений (3) и (5) с учетом (4) легко исключить неизвестную D, тогда:
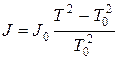 . (6)
. (6)
В формуле (6) осталась одна неизвестная величина – это момент инерции рамки 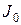 . Его можно найти, если измерить период колебаний рамки с эталонным телом
. Его можно найти, если измерить период колебаний рамки с эталонным телом 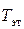 , момент инерции
, момент инерции 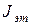 которого заранее известен:
которого заранее известен:
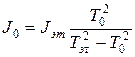 . (7)
. (7)
В качестве такого тела мы будем применять однородный куб. Его момент инерции относительно оси, проходящей через его центр масс равен:
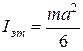 , (8)
, (8)
где m – масса, а – ребро куба. Из соотношений (6) и (8) получим формулу для расчета момента инерции тела, закрепленного в рамке:
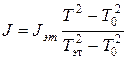 . (9)
. (9)
Как следует из формулы (1), момент инерции твердого тела зависит от ориентации оси вращения относительно его главных осей. Очевидно, что и период колебаний рамки с телом будет зависеть от ориентации тела по отношению к рамке:
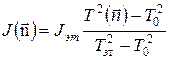 . (10)
. (10)
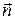 – направляющий вектор оси вращения (оси рамки).
– направляющий вектор оси вращения (оси рамки).
Теперь применим формулу (1), а также полученные выше формулы к различным твердым телам. Главные моменты куба равны между собой 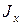 =
= 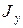 =
= 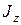 , поэтому при любом направлении оси вращения
, поэтому при любом направлении оси вращения 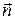 момент инерции куба относительно этой оси:
момент инерции куба относительно этой оси:
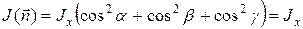 . (11)
. (11)
Периоды крутильных колебаний куба должны совпадать для всех осей вращения, проходящих через его центр масс.
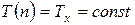 . (12)
. (12)
В случае симметричного прямоугольного параллелепипеда два главных момента совпадают между собой и не равны третьему:
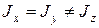 . (13)
. (13)
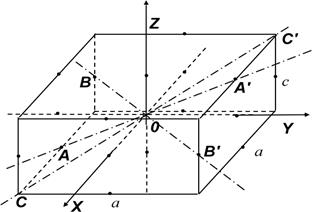 Поэтому периоды колебаний относительно главных осей OX и OY будут равны между собой и отличаются от колебаний вокруг оси OZ:
Поэтому периоды колебаний относительно главных осей OX и OY будут равны между собой и отличаются от колебаний вокруг оси OZ:
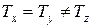 . (14)
. (14)
Рис. 8. Симметричный прямоугольный параллелепипед. Ось вращения CC ’ – пространственная диагональ. Диагонали, параллельные граням: AA ’ и BB ’.
На рисунке 8 показан симметричный прямоугольный параллелепипед со сторонами a и c. Найдем его моменты инерции относительно трех показанных на рисунке осей вращения. Относительно оси AA ’:
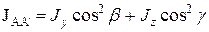 . (15)
. (15)
Направляющие косинусы оси вращения найдем из размеров тела:
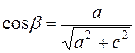 ,
, 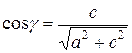 . (16)
. (16)
Из формул (15) и (16) очевидно, что
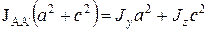 . (17)
. (17)
Относительно другой диагонали BB ’:
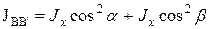 . (18)
. (18)
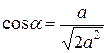 ,
, 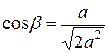 ,
, 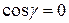 . (19)
. (19)
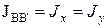 . (20)
. (20)
Теперь найдем момент инерции относительно большой диагонали CC ’:
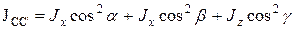 . (21)
. (21)
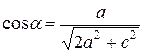 ,
, 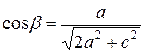 ,
, 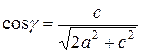 . (22)
. (22)
 Тогда
Тогда
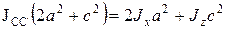 . (23)
. (23)
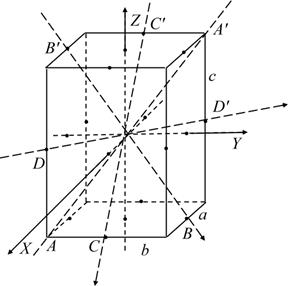
Рис. 9. Несимметричный прямоугольный параллелепипед. Ось вращения AA ’ – пространственная диагональ. Параллельные граням диагонали – BB ’, CC ’, DD ’.
Теперь запишем выражения, связывающие моменты инерции относительно диагоналей несимметричного прямоугольного параллелепипеда, показанных на рисунке 9 с его размерами и главными моментами.
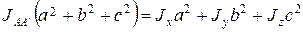 . (24)
. (24)
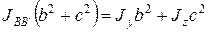 . (25)
. (25)
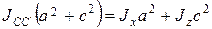 . (26)
. (26)
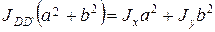 . (27)
. (27)
Исходя из формул, полученных в данной работе, можно доказать, что между периодами колебаний и направлением оси вращения существует зависимость:
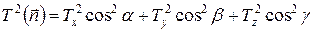 . (28)
. (28)
 2015-05-13
2015-05-13 4272
4272








