2015-05-13
13654
Показательным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью
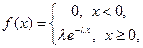(3.12)
где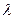 
постоянная положительная величина.
Функция распределения показательного закона (рис.2)
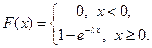(3.13)
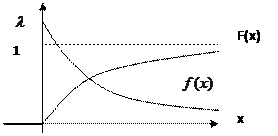
Рис. 2. Графики функции плотности вероятности
и функции распределения
Математическое ожидание, дисперсия, среднее квадратическое отклонение показательного закона распределения соответственно равны:
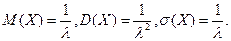
Пример 46. Написать плотность и функцию распределения показательного закона, если параметр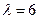 
.
Решение. Подставляя в последние две формулы, получаем, что
, 
.
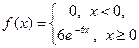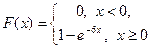Вероятность попадания в интервал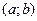 
случайной величины 
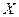, распределенной по показательному закону 
.
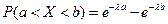Пример 47. Непрерывная случайная величина X распределена по показательному закону, заданному плотностью вероятност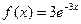и 
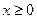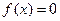при 
, 
при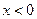 
Найдите вероятность того, что в результате испытания Х попадет в интервал (0,13; 0,7).
Решение. По условию, a = 0,13, b = 0,7,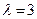 
.
Подставляя данные в формулу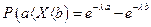 
, получаем, что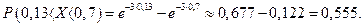 
Пример 48. Найдите математическое ожидание, дисперсию и среднее квадратическое отклонение показательного закона, заданного функцией распределения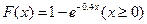 
.
Решение. Учитывая, что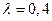 
получаем, что
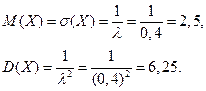
Пример 49. Испытывают два независимо работающих элемента. Длительность времени безотказной работы первого элемента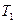 
имеет показательное распределение 
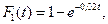второго – 
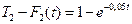. Найдите вероятность того, что за время длительностью 
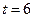ч: а) оба элемента откажут; б) оба элемента не откажут; в) только один элемент откажет; г) хотя бы один элемент откажет.
Решение
а) Вероятность отказа первого элемента: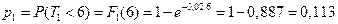 
.
Вероятность отказа второго элемента: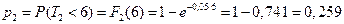 
.
Искомая вероятность того, что оба элемента откажут, по теореме умножения вероятностей: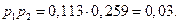 
б) Вероятность безотказной работы первого элемента: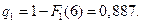 
Вероятность безотказной работы второго элемента: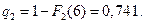 
Искомая вероятность безотказной работы обоих элементов: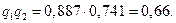 
в) Вероятность того, что откажет только один элемент: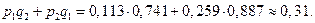 
г) Вероятность того, что хотя бы один элемент откажет:
