Функция распределения

Универсальным способом задания закона распределения, пригодным как для дискретных, так и для непрерывных случайных величин, является функция распределения.

Функцией распределения случайной величины X называется функция F (x), определяющая для каждого значения x вероятность того, что случайная величина X примет значение меньшее, чем x, то есть

F (x) = P (X < x).

Основные свойства функции распределения F (x):

1. Так как по определению F (x) равна вероятности события, все возможные значения функции распределения принадлежат отрезку [0; 1]:

0 £ F (x) £ 1.

2. Если 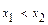, то 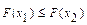, то есть F (x) – неубывающая функция своего аргумента.

3. Вероятность того, что случайная величина примет значение, принадлежащее полуинтервалу [ a, b), равна приращению функции распределения на этом интервале:

P (a £ X < b) = F (b) – F (a).

4. Если все возможные значения случайной величины принадлежат отрезку [ a, b ], то

F (x) = 0, при x £ a; F (x) = 1, при x > b.

Функция распределения дискретных случайных величин может быть определена по формуле

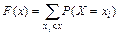. (15)

Если известен ряд распределения дискретной случайной величины, легко вычислить и построить ее функцию распределения. Продемонстрируем, как это делается на примере 23.

Пример 25. Вычислить и построить функцию распределения для дискретной случайной величины, закон распределения которой, имеет вид:

xi	0,1	1,2	2,3	4,5
pi	0,1	0,2	0,6	0,1

Решение. Определим значения функции F (x) = P (X < x) для всех возможных значений x:

при x Î (– ¥; 0,1] нет ни одного значения случайной величины X, меньшего данных значений x, то есть нет ни одного слагаемого в сумме (15):

F (x) = 0;

при x Î (0,1; 1,2] только одно возможное значение (X = 0,1) меньше рассматриваемых значений x. То есть при x Î (0,1; 1,2] F (x) = P (X = 0,1) = 0,1;

при x Î (1,2; 2,3] два значения (X = 0,1 и X = 1,2) меньше данных значений x, следовательно, F (x) = P (X = 0,1) + P (X = 1,2) = 0,1 + 0,2 = 0,3;

при x Î (2,3; 4,5] три значения (X = 0,1, X = 1,2 и X = 2,3) меньше данных значений x, следовательно, F (x) = P (X = 0,1) + P (X = 1,2) + P (X = 2,3) = 0,1 + 0,2 + 0,6 = 0,9;

при x Î (4,5, ¥) все возможные значения случайной величины X будут меньше данных значений x, и F (x) = P (X = 0,1) + P (X = 1,2) + P (X = 2,3) +

+ P (X = 4,5) = 0,1 + 0,2 + 0,6 + 0,1 = 1.

Таким образом,

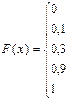
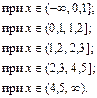
График функции F (x) изображен на рисунке 8.

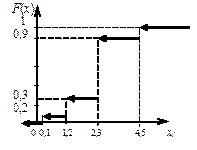Рисунок 8 – Функция распределения

В общем случае, функция распределения F (x) дискретной случайной величины X есть разрывная ступенчатая функция, непрерывная слева, скачки которой происходят в точках, соответствующих возможным значениям х ₁, х ₂, … случайной величины X и равны вероятностям p ₁, p ₂, … этих значений.

Функция распределения непрерывных случайных величин. Теперь можно дать более точное определение непрерывных случайных величин: случайная величина X называется непрерывной, если ее функция распределения F (x) при всех значениях x непрерывна и, кроме того, имеет производную 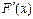всюду, за исключением, может быть, отдельных точек.

Из непрерывности функции F (x) следует, что вероятность каждого отдельного значения непрерывной случайной величины равна нулю.

Так как вероятность каждого отдельного значения непрерывной случайной величины равна 0, свойство 3 функции распределения для непрерывной случайной величины будет иметь вид

P (a £ X < b) = P (a £ X £ b) = P (a < X £ b) = P (a < X < b) = F (b) – F (a).

Пример 26. Вероятности поражения цели для каждого из двух стрелков соответственно равны: 0,7; 0,6. Случайная величина X – число промахов, при условии, что каждый стрелок сделал по одному выстрелу. Составить ряд распределения случайной величины X, построить столбцовую диаграмму и функцию распределения.

Решение. Возможные значения данной случайной величины X: 0, 1, 2. Условие задачи можно рассматривать как серию из n = 2 независимых испытаний. В данном случае для вычисления вероятностей возможных значений случайной величины X можно воспользоваться теоремами сложения вероятностей несовместных событий и умножения вероятностей независимых событий:

Обозначим события:

A _i = { i -й стрелок поразил мишень}, i = 1, 2.

Согласно условию, вероятность события A ₁ P (A ₁) = 0,7, вероятность события A ₂– P (A ₂) = 0,6. Тогда вероятности противоположных событий: , .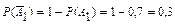

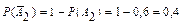Определим все элементарные события данного случайного эксперимента и соответствующие вероятности:

Элементарные события	События	Вероятности
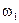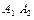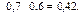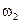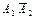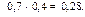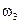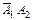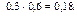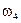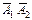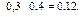Итого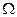

;

;

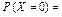
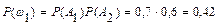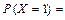
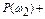
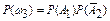
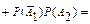
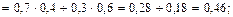
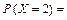
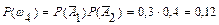(Проверим, что ).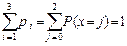

Ряд распределения данной случайной величины X имеет вид

xi				Итого
pi	0,42	0,46	0,12

Столбцовая диаграмма, соответствующая этому ряду распределения, приведена на рисунке 9.

Вычислим функцию распределения данной случайной величины:

:

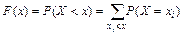при x Î (- ¥, 0] ;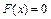

при x Î (0, 1] ;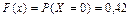

при x Î (1, 2] ;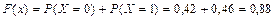

при x Î (2, +¥);

.

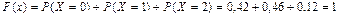Итак, функция распределения рассматриваемой случайной величины имеет вид:

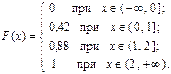
График функции F (x) приведён на рисунке 10.

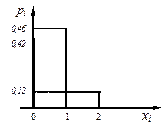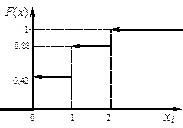Рисунок 9 – Столбцовая диаграмма	Рисунок 10 – Функция распределения

Функция плотности распределения вероятностей непрерывной случайной величины.

Плотностью распределения вероятностей непрерывной случайной величины X в точке x называется производная ее функции распределения в этой точке:

f (x) = F ¢(x).

По своему смыслу значения функции f (x) пропорциональны вероятности того, что исследуемая случайная величина примет значение где-то в непосредственной близости от точки x.

Функция плотности распределения f (x), как и функция распределения F (x), является одной из форм задания закона распределения, но она применима только для непрерывных случайных величин. Функцию плотности распределения вероятностей f (x) еще называют дифференциальной функцией распределения, тогда как функцию распределения F (x) называют, соответственно, интегральной функцией распределения.

График функции плотности распределения f (x) называется кривой распределения.

Рассмотрим свойства, которыми обладает функция плотности распределения непрерывной случайной величины.

Свойство 1. Плотность распределения вероятностей – неотрицательная функция:

f (x) ³ 0

(геометрически: кривая распределения лежит не ниже оси абсцисс).

Свойство 2. Вероятность попадания значения случайной величины на участок от a до b определяется по формуле

;

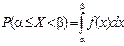(геометрически: эта вероятность равна площади криволинейной трапеции, ограниченной кривой f (x), осью Ох и прямыми x = a и x = b).

Свойство 3.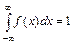

(геометрически: площадь фигуры, ограниченной кривой распределения и осью абсцисс, равна единице).

В частности, если все возможные значения случайной величины принадлежат отрезку [ a, b ], то

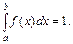
Свойство 4. Функция распределения F (x) может быть найдена по известной функции плотности распределения следующим образом:

.

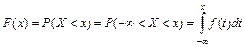Пример 27. Непрерывная случайная величина задана функцией распределения

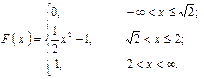
Определить дифференциальную функцию плотности распределения.

Решение. Определим дифференциальную функцию плотности распределения

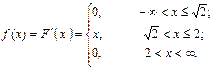
Пример 28. Является ли плотностью распределения некоторой случайной величины каждая из следующих функций?

а) 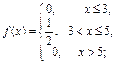б)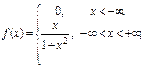

в)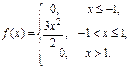

Решение. а) Проверим справедливость свойства 3: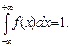

В данном случае имеем

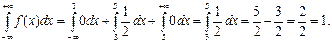
Функция неотрицательна для всех x. То есть заданная функция является функцией плотности распределения некоторой случайной величины.

б) Заданная функция не является плотностью распределения некоторой случайной величины, так как .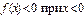

в) Проверим справедливость свойства 3: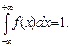

В данном случае имеем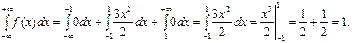

Функция неотрицательна для всех 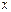. То есть заданная функция является функцией плотности распределения некоторой случайной величины.

Вопросы для самоконтроля

1. Что называется случайной величиной?

2. Какие величины называются дискретными? непрерывными?

3. Что называется законом распределения случайной величины?

4. Какими способами может быть задан закон распределения дискретной случай­ной величины? непрерывной?

5. Что характеризует функция распределения F(x) случайной величины?

6. Как определить вероятность попадания значения случайной величины в некоторый интервал с помощью функции распределения?

7. Что характеризует функция плотности распределения случайной величины? Укажите ее вероятностный смысл.

8. Для каких величин определена функция плотности распределения?

9. Может ли функция плотности распределения принимать отрицательные зна­чения?

10. Как связаны между собой функции F(x) и f (x)?

11. Какие случайные величины называются непрерывными?

12. Чему равна площадь фигуры, ограниченной кривой распределения и осью абсцисс?

13. Как определить вероятность попадания значения непрерывной случайной ве­личины в некоторый интервал с помощью функции плотности распределения?