Нормальным называют распределение вероятностей непрерывной случайной величины 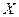 , плотность которого имеет вид:
, плотность которого имеет вид:
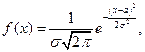 где
где 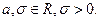 (3.16)
(3.16)
При этом – 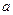 математическое ожидание,
математическое ожидание, 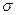 среднее квадратическое отклонение этой случайной величины.
среднее квадратическое отклонение этой случайной величины.
Вероятность того, что 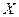 примет значение, принадлежащее интервалу
примет значение, принадлежащее интервалу 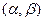 , равна:
, равна:
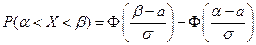 , где
, где 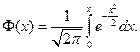 (3.17)
(3.17)
Вероятность того, что отклонение случайной величины X, распределенной по нормальному закону, от математического ожидания а, не превысит по абсолютной величине 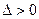 , равна:
, равна: 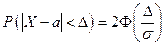 .
.
Следствие («правило трех сигм»). Если случайная величина X распределена нормально (с параметрами а и 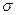 ), то практически достоверно, что абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения, т. е.
), то практически достоверно, что абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего квадратического отклонения, т. е. 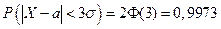 .
.
Другими словами, если случайная величина X имеет нормальный закон распределения с параметрами а и 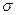 , то практически достоверно, что ее значения заключены в интервале
, то практически достоверно, что ее значения заключены в интервале 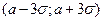 .
.
Пример 52. Математическое ожидание и среднее квадратическое отклонение нормально распределенной случайной величины 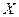 соответственно равны 10 и 2. Найдите вероятность того, что в результате испытания
соответственно равны 10 и 2. Найдите вероятность того, что в результате испытания 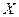 примет значение, заключенное в интервале (12,14).
примет значение, заключенное в интервале (12,14).
Решение. Воспользуемся формулой 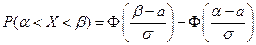 . Подставив
. Подставив 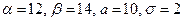 , получим:
, получим: 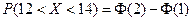 .
.
По таблице приложения 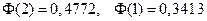 . Искомая вероятность
. Искомая вероятность 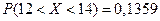 .
.
Пример 53. Производится измерение диаметра вала без систематических (одного знака) ошибок. Случайные ошибки измерения подчинены нормальному закону со средним квадратическим отклонением 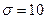 мм. Найдите вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине 15 мм.
мм. Найдите вероятность того, что измерение будет произведено с ошибкой, не превосходящей по абсолютной величине 15 мм.
Решение. Математическое ожидание случайных ошибок равно нулю, поэтому 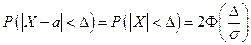 . Положив
. Положив 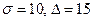 , находим
, находим 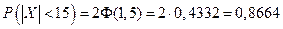 .
.
 2015-05-13
2015-05-13 5698
5698
