Решение задач по кинематике необходимо начинать с определения типа движения тела (материальной точки). Подавляющее большинство задач можно отнести к одному из следующих типов простейших движений материальной точки: прямолинейное равномерное или равнопеременное движение, равномерное или равнопеременное вращение. В большинстве задач, в особенности в случае криволинейного движения на плоскости, следует изобразить на рисунке координатные оси, направления скоростей и ускорений. После этого необходимо выписать соответствующие уравнения с учетом условий данной задачи и затем решить полученную систему. Рассмотрим методы решения задач по кинематике на конкретных примерах.
Задача 1. На дорогу от пункта А до пункта Б водитель обычно тратит время 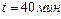 . Однако в часы пик, чтобы ехать с привычной скоростью, ему приходится выбирать другой маршрут. Этот путь на
. Однако в часы пик, чтобы ехать с привычной скоростью, ему приходится выбирать другой маршрут. Этот путь на 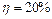 длиннее и
длиннее и 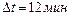 занимают остановки. Все равно водитель экономит
занимают остановки. Все равно водитель экономит 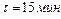 . Во сколько раз его скорость в часы пик меньше его обычной скорости?
. Во сколько раз его скорость в часы пик меньше его обычной скорости?
Решение
Данная задача относится к случаю равномерного движения и решается исходя из определения средней скорости. Пусть расстояние от А до Б равно 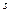 , скорость автомобили в обычное время
, скорость автомобили в обычное время 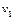 , а в часы пик
, а в часы пик 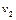 . Тогда, согласно условию, для движения в обычное время
. Тогда, согласно условию, для движения в обычное время 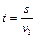 . Если бы в часы пик автомобиль двигался по прежнему маршруту, то на это было бы затрачено время
. Если бы в часы пик автомобиль двигался по прежнему маршруту, то на это было бы затрачено время 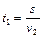 , в действительности же с учетом удлинения маршрута и движения с обычной скоростью на дорогу было затрачено
, в действительности же с учетом удлинения маршрута и движения с обычной скоростью на дорогу было затрачено 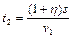 . С учетом времени, затраченного на остановки и сэкономленных минут, получаем уравнение
. С учетом времени, затраченного на остановки и сэкономленных минут, получаем уравнение
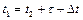
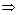
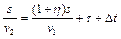 . (1.1.1)
. (1.1.1)
Подставляя в (1.1.1) 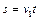 , находим
, находим
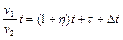 .
.
Отсюда получаем для отношения скоростей выражение
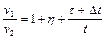 .
.
Подставляя числовые значения, находим
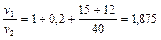 .
.
Таким образом, скорость автомобиля в часы пик в 1,875 раза меньше его скорости в обычное время.
Задача 2. Пассажир поднимается по неподвижному эскалатору метро за время 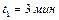 , а по движущемуся вверх эскалатору за время
, а по движущемуся вверх эскалатору за время 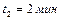 . Сможет ли он подняться по эскалатору, движущемуся с той же скоростью вниз? Если сможет, то за какое время?
. Сможет ли он подняться по эскалатору, движущемуся с той же скоростью вниз? Если сможет, то за какое время?
Решение
Рассматриваемая задача также относится к типу задач на равномерное движение. Отличие от предыдущей заключается в том, что здесь необходимо правильно записывать все скорости в неподвижной системе отсчета (относительность движения). Пусть длина эскалатора равна 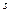 , а скорости эскалатора относительно земли и человека относительно эскалатора равны соответственно
, а скорости эскалатора относительно земли и человека относительно эскалатора равны соответственно 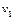 и
и 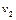 . Тогда для первых двух случаев можно написать уравнения равномерного движения
. Тогда для первых двух случаев можно написать уравнения равномерного движения
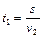 ,
, 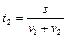 . (1.1.2)
. (1.1.2)
Аналогично для движения человека по движущемуся ему навстречу эскалатору
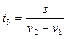 . (1.1.3)
. (1.1.3)
Разрешая (1.1.2) относительно скоростей, находим
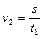 ,
, 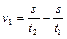 . (1.1.4)
. (1.1.4)
Подставляя (1.1.4) в (1.1.3) получаем 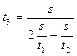 , откуда после несложных алгебраических преобразований следует
, откуда после несложных алгебраических преобразований следует
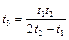 .
.
После подстановки числовых значений находим
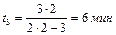 .
.
Полученный ответ означает, что человек сможет подняться по движущемуся ему навстречу эскалатору (об этом свидетельствует положительный знак ответа) и сделает это за 6 минут.
Задача 3. Самолет совершает прямой и обратный рейсы между двумя населенными пунктами. При каком направлении ветра относительно трассы время полета будет максимальным? минимальным?
Решение
 |
|
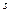 , собственную скорость самолета (относительно воздуха) и скорость ветра (относительно земли) соответственно через
, собственную скорость самолета (относительно воздуха) и скорость ветра (относительно земли) соответственно через 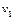 и
и 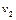 , а углы, которые образуют векторы
, а углы, которые образуют векторы 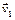 и
и 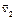 с вектором
с вектором 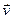 скорости самолета относительно земли, через
скорости самолета относительно земли, через 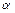 и
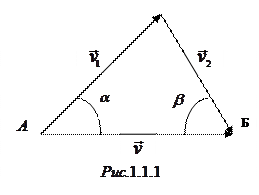
и 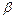 соответственно (рис. 1.1.1). Проектируя векторы скоростей на направления полета самолета и перпендикулярное к нему, получаем уравнения
соответственно (рис. 1.1.1). Проектируя векторы скоростей на направления полета самолета и перпендикулярное к нему, получаем уравнения 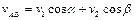 (по ветру),
(по ветру), 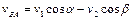 (против ветра),
(против ветра), 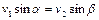 . (1.1.5)
. (1.1.5)
Общее время движения, очевидно, равно
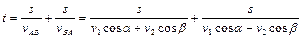 . (1.1.6)
. (1.1.6)
Исключая из (1.1.6) угол 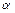 при помощи (1.1.5) и основного тригонометрического тождества, преобразуем (1.1.6) к виду
при помощи (1.1.5) и основного тригонометрического тождества, преобразуем (1.1.6) к виду
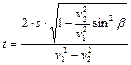 .
.
Учитывая элементарные свойства тригонометрических функций, приходим к выводу, что наименьшее время полета будет в случае, когда 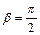 , т.е. когда ветер дует перпендикулярно направлению полета. Если же
, т.е. когда ветер дует перпендикулярно направлению полета. Если же 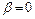 время полета будет максимальным.
время полета будет максимальным.
Задача 4. Частица пролетает расстояние 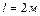 равномерно, а затем тормозит с ускорением
равномерно, а затем тормозит с ускорением 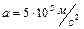 . При какой начальной скорости частицы время ее движения от вылета до остановки будет наименьшим?
. При какой начальной скорости частицы время ее движения от вылета до остановки будет наименьшим?
Решение
Пусть начальная скорость частицы равна 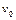 . Тогда время ее равномерного движения
. Тогда время ее равномерного движения 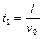 . Из уравнения скорости равнозамедленного движения
. Из уравнения скорости равнозамедленного движения 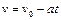 находим время движения
находим время движения 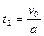 . Следовательно, общее время движения
. Следовательно, общее время движения
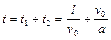 . (1.1.7)
. (1.1.7)
Исследуем функцию 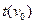 на экстремум:
на экстремум:
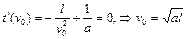 .
.
Так как производная в окрестности критической точки меняет знак с минуса на плюс, полученное значение 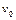 обеспечивает минимальное время движения частицы от момента вылета до остановки. Подставляя числовые значения, получаем:
обеспечивает минимальное время движения частицы от момента вылета до остановки. Подставляя числовые значения, получаем:
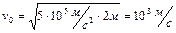 .
.
Задача 5. Тело, свободно падающее с некоторой высоты, первый участок пути проходит за время 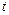 , а такой же последний – за время
, а такой же последний – за время 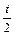 . Определить высоту, с которой падало тело.
. Определить высоту, с которой падало тело.
Решение
Пусть все время падения тела равно 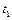 , тогда высота падения тела
, тогда высота падения тела
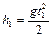 . (1.1.8)
. (1.1.8)
За время 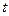 тело пролетает расстояние
тело пролетает расстояние
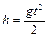 , (1.1.9)
, (1.1.9)
а за время 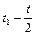 - расстояние
- расстояние
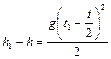 . (1.1.10)
. (1.1.10)
После подстановки (1.1.8) и (1.1.9) в (1.1.10) получаем 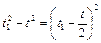 . Решая это уравнение, находим
. Решая это уравнение, находим 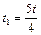 , следовательно, высота падения тела
, следовательно, высота падения тела
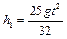 .
.
Задача 6. Частица движется в положительном направлении оси 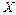 так, что ее скорость изменяется по закону
так, что ее скорость изменяется по закону 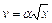 , где
, где 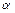 - положительная постоянная. Имея в виду, что в момент времени
- положительная постоянная. Имея в виду, что в момент времени 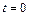 она находилась в точке
она находилась в точке 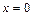 , найти: зависимость скорости и ускорения частицы от времени; среднюю скорость частицы за время, в течение которого она пройдет
, найти: зависимость скорости и ускорения частицы от времени; среднюю скорость частицы за время, в течение которого она пройдет 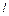 метров пути.
метров пути.
Решение
Согласно определению скорости 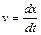 . Таким образом, закон движения частицы можно найти, интегрируя уравнение
. Таким образом, закон движения частицы можно найти, интегрируя уравнение 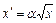 с начальным условием
с начальным условием 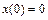 . Разделяя переменные, получаем
. Разделяя переменные, получаем 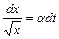 , а после интегрирования
, а после интегрирования 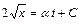 . Подстановка начального условия дает
. Подстановка начального условия дает 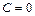 , что позволяет записать закон движения частицы в виде
, что позволяет записать закон движения частицы в виде 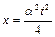 . Используя полученный результат, находим зависимости скорости и ускорения от времени:
. Используя полученный результат, находим зависимости скорости и ускорения от времени:
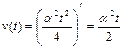 ,
, 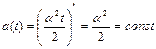 .
.
Для ответа на последний вопрос задачи определим время, необходимое частице для преодоления 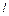 метров пути:
метров пути: 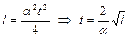 . Тогда, используя определение средней скорости, получаем
. Тогда, используя определение средней скорости, получаем
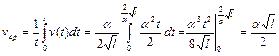 .
.
Задача 7. Закон движения материальной точки имеет вид 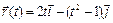 . Найти уравнение траектории, закон изменения скорости и ускорения от времени.
. Найти уравнение траектории, закон изменения скорости и ускорения от времени.
Решение
Из закона изменения радиус-вектора от времени находим зависимости координат от времени:
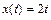 ,
, 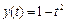 . (1.1.11)
. (1.1.11)
Исключая из (1.1.11) время, получаем уравнение траектории:
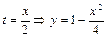 .
.
Законы изменения скорости и ускорения от времени находятся по определению:
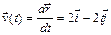 ,
, 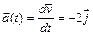 .
.
Зависимость от времени модулей этих величин устанавливается по формулам
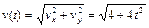 ,
, 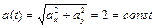 .
.
Задача 8. Угол поворота диска радиусом 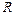 изменяется со временем по закону
изменяется со временем по закону 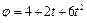 . Определить зависимости от времени угловой скорости, углового ускорения и линейной скорости точек, находящихся на краю диска. В какой момент времени угол между векторами скорости и ускорения будет составлять
. Определить зависимости от времени угловой скорости, углового ускорения и линейной скорости точек, находящихся на краю диска. В какой момент времени угол между векторами скорости и ускорения будет составлять 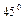 ?
?
Решение
Зависимости от времени угловой скорости и углового ускорения находим согласно определениям этих величин:
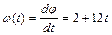 ,
, 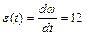 .
.
Для получения зависимости от времени линейной скорости используем связь между линейными и угловыми величинами:
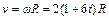 .
.
Вектор скорости в любой момент времени направлен по касательной к поверхности диска, а вектор ускорения все время изменяется по величине и направлению в соответствии с тем, как меняются нормальное и касательное ускорения. Угол между векторами скорости и ускорения будет составлять 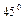 в тот момент, когда нормальное ускорение станет равным касательному (тогда треугольник ускорений становится равнобедренным).
в тот момент, когда нормальное ускорение станет равным касательному (тогда треугольник ускорений становится равнобедренным).
Нормальное ускорение можно определить по формуле
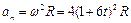 , (1.1.12)
, (1.1.12)
а касательное – по формуле
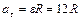 . (1.1.13)
. (1.1.13)
Приравнивая правые части (1.1.12) и (1.1.13), получаем
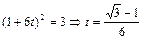 .
.
Задача 9. С самолета, летящего горизонтально со скоростью 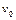 на высоте
на высоте 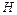 , сброшен груз. На какой высоте
, сброшен груз. На какой высоте 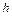 скорость груза будет направлена под углом
скорость груза будет направлена под углом 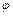 к горизонту? Найти радиус кривизны
к горизонту? Найти радиус кривизны 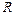 траектории на данной высоте. Чему равно расстояние
траектории на данной высоте. Чему равно расстояние 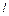 между грузом и самолетом в момент падения груза на землю?
между грузом и самолетом в момент падения груза на землю?
Решение
Направим оси 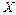 и
и 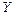 горизонтально и вертикально вниз. Угол, который образует вектор скорости с горизонтом, можно определить из треугольника скоростей (рис.1.1.2), из которого следует
горизонтально и вертикально вниз. Угол, который образует вектор скорости с горизонтом, можно определить из треугольника скоростей (рис.1.1.2), из которого следует 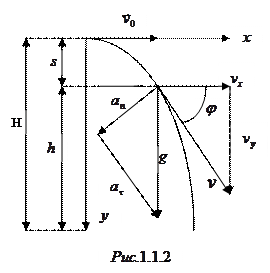
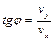 . (1.1.14)
. (1.1.14)
Если пренебречь сопротивлением воздуха, движение по горизонтали будет равномерным со скоростью 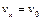 , а по вертикали – равноускоренным со скоростью
, а по вертикали – равноускоренным со скоростью 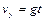 . Так как перемещение в вертикальном направлении за время
. Так как перемещение в вертикальном направлении за время 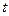 составит
составит 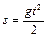 , то
, то
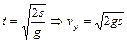 .
.
Подставляя полученные выражения в (1.1.14), находим
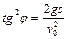 ,
,
а поскольку 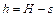 , то искомая высота определяется по формуле
, то искомая высота определяется по формуле
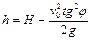 .
.
Для определения радиуса кривизны траектории на данной высоте воспользуемся треугольниками скоростей и ускорений. Из рисунка (1.1.2) видно, что
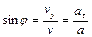 ,
, 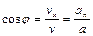 .
.
Поскольку полное ускорение груза равно ускорению свободного падения 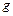 , нормальное ускорение по определению
, нормальное ускорение по определению 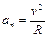 , а модуль скорости
, а модуль скорости 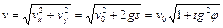 , получаем
, получаем
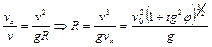 .
.
Так как в пренебрежении сопротивлением воздуха горизонтальные скорости груза и самолета будут одинаковы, их перемещение друг относительно друга будет происходить строго по вертикали, и в момент приземления груза расстояние между ним и самолетом составит 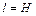 .
.
Задача 10. Тело брошено под углом к горизонту так, что его радиус-вектор изменяется по закону 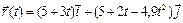 . Ось
. Ось 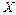 направлена вдоль поверхности земли, ось
направлена вдоль поверхности земли, ось 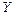 - вертикально вверх. Под каким углом к горизонту
- вертикально вверх. Под каким углом к горизонту 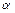 брошено тело? Какова дальность полета и максимальная высота полета тела? Определить радиус кривизны траектории в ее верхней точке.
брошено тело? Какова дальность полета и максимальная высота полета тела? Определить радиус кривизны траектории в ее верхней точке.
Решение
Из уравнения движения тела можно определить законы изменения со временем координат тела:
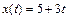 ,
, 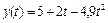 .
.
Используя определение скорости, находим уравнения проекций вектора скорости на оси 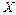 и
и 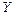 :
:
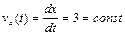 ,
, 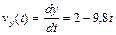 .
.
В начальный момент времени 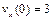 ,
, 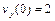 , следовательно, для угла бросания получаем
, следовательно, для угла бросания получаем
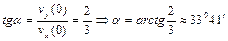 .
.
В момент приземления 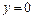 ; решая квадратное уравнение, находим время полета тела:
; решая квадратное уравнение, находим время полета тела:
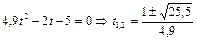 .
.
Очевидно, моменту приземления соответствует знак плюс перед корнем, следовательно, 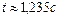 . Подставляя полученное значение в уравнение горизонтального движения, находим дальность полета
. Подставляя полученное значение в уравнение горизонтального движения, находим дальность полета
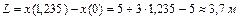 .
.
В верхней точке траектории вектор скорости направлен горизонтально, следовательно, 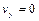 , откуда находим время подъема тела до верхней точки траектории
, откуда находим время подъема тела до верхней точки траектории
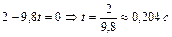 .
.
Подставляя найденное значение в уравнение вертикального движения, находим максимальную высоту подъема тела
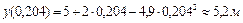 .
.
Так как в верхней точке траектории модуль скорости тела 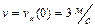 , а нормальное ускорение равно полному (которое в любой точке траектории равно ускорению свободного падения
, а нормальное ускорение равно полному (которое в любой точке траектории равно ускорению свободного падения 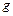 ), из определения нормального ускорения находим радиус кривизны траектории в ее верхней точке
), из определения нормального ускорения находим радиус кривизны траектории в ее верхней точке
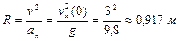 .
.
 2015-05-13
2015-05-13 4752
4752
