Модель хищник – жертва Вольтерра

Один вид является хищником по отношению друг к другу:

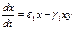
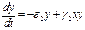
Найдем координаты особой точки

e₁х - g₁хy = 0; x× (e₁ - g₁y) = 0;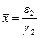

- e₂у - g₂хy = 0 -y× (e₂ - g₂х) = 0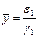

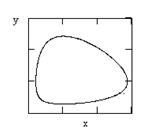
В этом случае фазовые траектории вблизи особой точки представляют собой концентрические эллипсы, а сама особая точка является центром. Вдали от особой точки фазовые траектории являются замкнутыми, хотя их форма отличается от эллипсовидной.

Особая точка типа центр является в целом неустойчивой точкой.

Пусть колебания 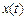и 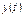происходят таким образом, что изображающая точка движется по фазовой траектории 1.

В момент времени, когда точка находится в положении М, в систему извне добавляют некоторое число особей Dу, такое, что изображающая точка переходит скачком из точки М в точку М¢. После этого, если система будет предоставлена самой себе, колебания х(t),у(t) уже будут происходить с большими амплитудами, чем прежде.

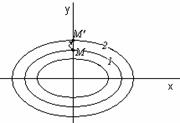Изображающая точка будет двигаться по траектории (2). Таким образом, колебания в системе неустойчивые, меняют свои характеристики при внешнем воздействии. Ситуации часто наблюдались на практике. Можно было бы показать, что результат получится более обнадеживающим, если истребления хищника вести сезонно, согласуя сезоны охоты с характером цикла.

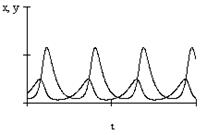
На рисунке приведены графики функций х(t), у(t). Видно, что х(t) и у(t) являются периодическими функциями времени, причем максимум численности жертв всегда опережает максимум численности хищников.

На основе рассмотренной системы можно конструировать более сложные модели. Так, можно учесть внутривидовую конкуренцию:

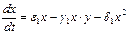
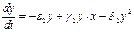
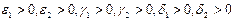
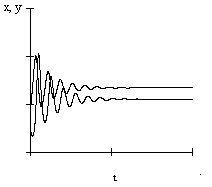
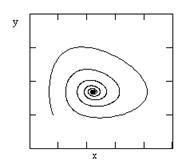
Допустим, что параметры системы изменяются таким образом, что условие превращается в равенство. В этом случае особая точка будет лежать на границе устойчивых фокусов и узлов. При изменении знака неравенства на обратный в системе происходит бифуркация– особая точка становится устойчивым узлом.

Можно рассмотреть сосуществование не двух, а нескольких видов. В этом случае получим систему:

,

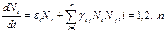где числа 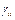характеризует взаимоотношение 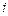–го и 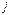–го вида. Число 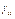отрицательно, если і –й вид служит пищей для j –ого и положителен в противном случае. Если виды нейтральны по отношению друг к другу, то 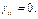Наконец, неположительное число 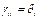- коэффициент внутривидовой конкуренции.