Умножение вектора на скаляр
Операция 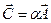 называется умножением вектора на скаляр. При такой операции длина вектора увеличивается в
называется умножением вектора на скаляр. При такой операции длина вектора увеличивается в 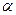 раз, а направление вектора сохраняется. В декартовой системе координат:
раз, а направление вектора сохраняется. В декартовой системе координат: 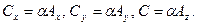
Сложение векторов
Суммой двух векторов 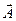 и
и 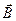 является новый вектор
является новый вектор 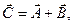 у которого проекции равны суммам соответствующих проекций векторов
у которого проекции равны суммам соответствующих проекций векторов 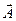 и
и 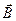 :
:
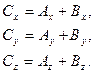
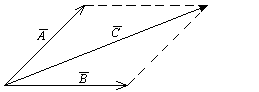
Геометрическим представлением сложения векторов является правило параллелограмма.
Вычитание векторов
Вычитание двух векторов является операция обратная сложению: 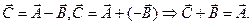
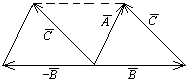
Геометрическим представлением вектора 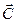 является вектор, соединяющий конец вектора
является вектор, соединяющий конец вектора 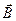 и
и 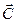 .
.
Из двух векторов 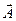 и
и 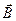 можно образовать скалярное произведение:
можно образовать скалярное произведение:
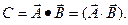
Величина скалярного произведения равна:
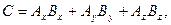
или 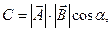 здесь
здесь 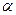 - угол между векторами
- угол между векторами 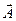 и
и 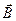 .
.
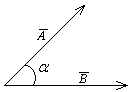
Операция векторного произведения из двух векторов 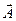 и
и 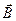 образует новый вектор:
образует новый вектор: 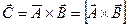 .Модуль векторного произведения равен
.Модуль векторного произведения равен 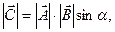 здесь
здесь 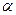 -угол между векторами
-угол между векторами 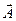 и
и 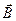 .
.
Геометрически модуль векторного произведения равен площади параллелограмма, построенного на векторах 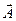 и
и 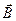 .
.
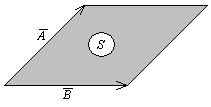
Направление векторного произведения определяется правилом правого винта: если головку винта вращать в плоскости векторов 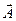 и
и 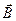 по кратчайшему направлению от вектора
по кратчайшему направлению от вектора 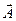 к вектору
к вектору 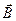 , то направление хода винта укажет направление вектора
, то направление хода винта укажет направление вектора 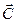 . Из этого определения следует, что вектор
. Из этого определения следует, что вектор 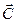 перпендикулярен плоскости векторов
перпендикулярен плоскости векторов 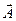 и
и 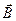 .
.
Проекции вектора 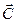 определяются с помощью определителя:
определяются с помощью определителя:
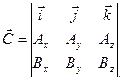
Откуда следует, что:
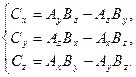
Основные векторные тождества:
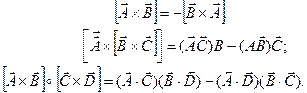
7.2.Таблицы производных и интегралов
| ФУНКЦИЯ | ПРОИЗВОДНАЯ |
| xn | nxn-1 |
| 1/x | -1/x2 |
| 1/xn | -n/xn+1 |
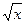 | 1/2 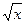 |
| eX | ex |
| exn | nenx |
| aX | ax lna |
| ln x | 1/x |
| sin x | cos x |
| cos x | - sin x |
| tg x | 1/cos2 x |
| ctg x | - 1/sin2 x |
| vu | u'/2vu |
| ln u | u'/u |
| u/v | (vu'-v'u)/v2 |
| arcsin x | 1/ 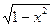 |
| arccos x | -1/ 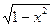 |
| arctg x | 1/(1+x2) |
| arcctg x | -1/(1+x2) |
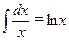 ;
; 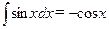 ;
;
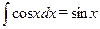 ;
; 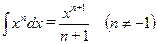 ;
;
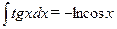 ;
; 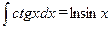 ;
;
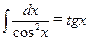 ;
; 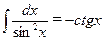 ;
;
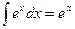 ;
; 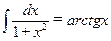 ;
;
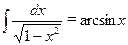 ;
; 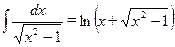 ;
; 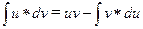 .
.
 2015-05-13
2015-05-13 3967
3967
