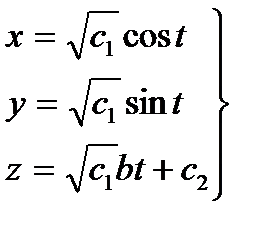 (3.4)
(3.4)
Точке (1,0,0) соответствует значение параметра t, равное нулю. Полагая t=0 в системе (3.4), получим
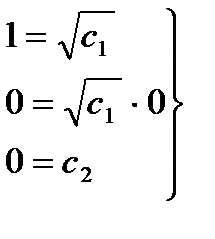
Откуда находим с1=1, с2=0,и значит параметрические уравнения векторной линии, проходящей через точку (1,0,0), будут

-это винтовая линия.
Векторное поле называется плоским, если все векторы 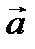 расположены в параллельных плоскостях и поле одно и тоже в каждой из этих плоскостей.
расположены в параллельных плоскостях и поле одно и тоже в каждой из этих плоскостей.
Если в какой-либо из этих плоскостей ввести декартову систему координат ХОУ, то векторы поля не будут содержать компоненты по оси OZ и координаты вектора не будут зависеть от z, то есть
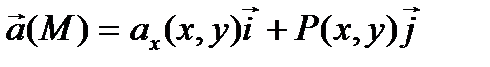 . Дифференциальные уравнения векторных линий плоского поля будут иметь вид:
. Дифференциальные уравнения векторных линий плоского поля будут иметь вид: 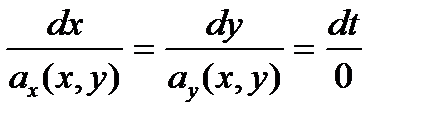 или
или
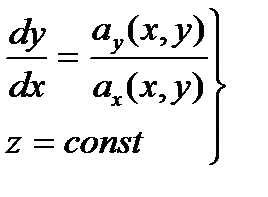
Отсюда видно, что векторные линии плоского поля являются плоскими, лежащими в плоскостях, параллельных плоскости ХОУ.
Пример 3.3. Найти векторные линии магнитного поля бесконечного проводника тока.
Решение. Будем считать, что проводник направлен по оси OZ и в этом же направлении течет ток I. Вектор напряженности Н магнитного поля, создаваемого током, равен
Н= 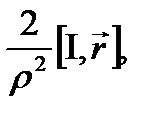 (3.5)
(3.5)
где I=I∙K есть вектор тока, r-радиус-вектор точки M(x,y,z), 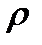 -расстояние от оси провода до точки М. Раскрывая векторное произведение (3.5), получим
-расстояние от оси провода до точки М. Раскрывая векторное произведение (3.5), получим 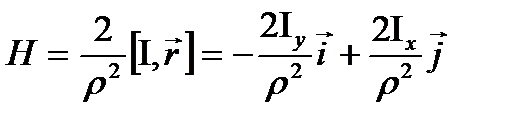 .
.
Дифференциальные уравнения векторных линий 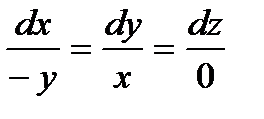 откуда
откуда 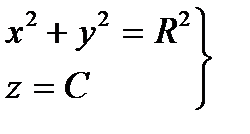 , то есть векторные линии являются окружностями с центрами на оси OZ.
, то есть векторные линии являются окружностями с центрами на оси OZ.
Пример 3.4. Найти векторные линии следующего поля 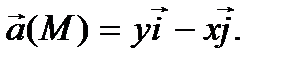
Решение. Составим дифференциальное уравнение 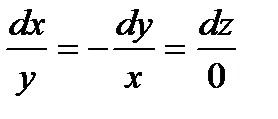 , интегрируя, получим
, интегрируя, получим 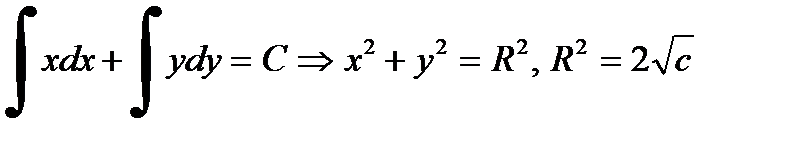 ,
, 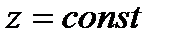 . То есть
. То есть 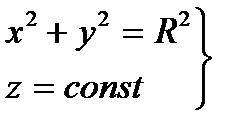
Дифференциальные уравнения векторных линий 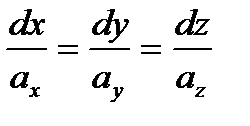 , могут быть записаны так:
, могут быть записаны так: 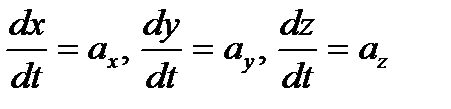 или в векторной форме:
или в векторной форме:
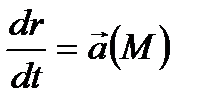 , (3.6)
, (3.6)
где 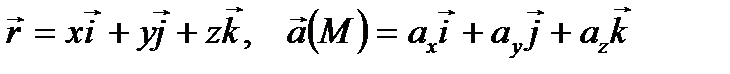 . Эта форма уравнений векторных линий оказывается удобной при решении подобных задач.
. Эта форма уравнений векторных линий оказывается удобной при решении подобных задач.
Пример 3.5. Найти векторные линии поля 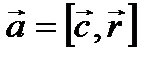 , где
, где  -постоянный вектор.
-постоянный вектор.
Решение. Применяя соотношения (3.6), получим
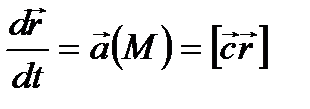 (3.7)
(3.7)
Умножая обе части (3.7) скалярно на 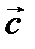 и используя свойства смешанного произведения, находим
и используя свойства смешанного произведения, находим
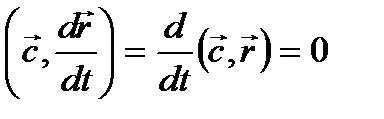 (3.8)
(3.8)
Аналогично, умножая обе части (13.7) скалярно на 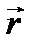 , получим
, получим
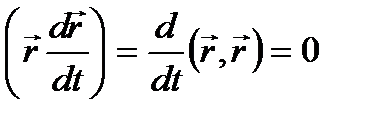 (3.9)
(3.9)
Из уравнения (3.8) следует, что 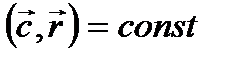 , а из уравнения (3.9) следует, что
, а из уравнения (3.9) следует, что 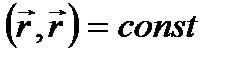 . Векторные линии являются линиями пересечения плоскостей
. Векторные линии являются линиями пересечения плоскостей 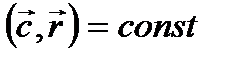 со сферами
со сферами 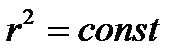 .
.
 2015-03-07
2015-03-07 1840
1840
