Обусловленность матрицы

При исследовании численных методов для решения математических задач необходимо различать свойства самой задачи и свойства вычислительного алгоритма. Для каждой математической задачи принято рассматривать вопрос о ее корректности.

Определение. Говорят, что задача поставлена корректно, если ее решение существует, единственно и непрерывно зависит от входных данных.

Рассмотрим систему

A x = f, (6.1)

где А - квадратная, неособенная матрица размерности n, и, следовательно, det(A) ≠ 0, тогда существует единственное решение системы. Чтобы убедиться в корректности задачи (6.1) необходимо еще установить непрерывную зависимость решения от входных данных. Входными данными являются правая часть f и элементы матрицы А.

Соответственно, различают устойчивость по правой части, когда возмущается только правая часть f, а матрица А остается неизменной, и коэффициентную устойчивость, когда возмущается только матрица А.

Будем считать, что решение и правая часть задачи (6.1) принадлежат линейному пространству H, состоящему из n -мерных векторов. Введем в H норму, для которой выполнено:

|| x ||>0, для всех х ≠0 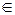H,

|| α x ||=| α | || x ||, для любого числа А и х 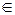H,

|| x+y ||≤|| x ||+|| y ||, для любых x и y 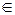H.

Определение. Нормой матрицы А, подчиненной данной норме векторов, называется число 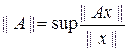, для всех х ≠0 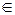H.

Наряду с системой (6.1) рассмотрим «возмущенную» систему A x_ε = f_δ, которая отличается от (6.1) правой частью. Насколько сильно может измениться решение х в результате изменения правой части?

Обозначим δx=x - x_ε,, δf=f - f_δ.

Определение. Говорят, что система (6.1) устойчива по правой части, если при любых f и f_δ справедлива оценка || δx|| ≤ M || δf ||, где M - постоянная, M >0.

Эта оценка выражает факт непрерывной зависимости решения от правой части, то есть показывает, что || δx|| стремится к нулю при || δf || стремящемся к нулю. Наличие устойчивости очень важно при численном решении систем уравнений, так как никогда нельзя задать правую часть f точно. Погрешность δf возникает в результате округления.

Получим оценку для относительной погрешности решения 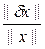. Используем неравенство ||f|| ≤ ||A|| ||x||. Перемножим его с неравенством || δx|| ≤ ||A^-1|| || δf ||, получим требуемую оценку

.

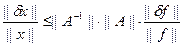Определение. Число ρ(A)= 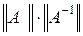называется числом обусловленности матрицы A и характеризует степень зависимости относительной погрешности решения от относительной погрешности правой части. В случае самосопряженной матрицы A =A^* это число равно

ρ(A)= ,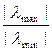

где λ_max, λ_min – максимальное и минимальное по модулю собственные значения матрицы A.

Матрицы с большим числом обусловленности называются плохо обусловленными. При численном решении систем с такими матрицами возможно сильное накопление погрешности. При небольших изменениях правой части погрешность решения может оказаться значительной.

Например, для матрицы

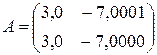
число обусловленности ρ(A)= 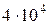, и если взять за правую часть системы вектор f= (1,0000, 1,0000) ^T, то получим решение x= (0,3333, 0,0000) ^T. Решение «возмущенной» системы с правой частью f_δ = (0,9998, 1,0000) ^T равно x_ε= (5,0000, 2,0000) ^T.

Если взять матрицу

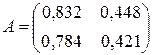
и за правую часть системы вектор f= (1,0000, 0) ^T, то получим решение 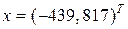. Решение «возмущенной» системы при изменении коэффициента a₂₂ = 0,421 на 0,433 равно x_ε = (47,983, -86,879) ^T.