Каноническая форма задачи; базисное решение

Основной метод решения задачи (3) - симплекс-метод обычно применяется к ограничениям в виде равенства, т. е. Ax = b, x ≥ 0. Такая форма задачи называется канонической. Для ее построения неравенства исходной задачи преобразовываются в равенства с помощью искусственных переменных, которые также являются неотрицательными. В результате этого действия происходит расширение области решений исходной задачи, другими словами, она становится подмножеством области решения новой – канонической задачи

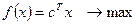, (6)

Ax = b

х ≥ 0

где для простоты будем считать, что по-прежнему векторы х и c имеет размерность (mx1), матрица А имеет размерность (mxn), причем, m < п. а вектор b – размерность (mx),

Отметим, что область решений канонической задачи сохраняет основные геометрические свойства области исходной задачи, т. е. содержит ее в виде своего подмножества.

При решении задачи (3) понятия базис и базисное решение играют ключевую роль в организации поиска оптимального решения, если оно существует. С их помощью генерируются очередные вершины области допустимых решений, и организуется переход из одной вершины в другую. Удачный выбор начального базиса и базисного решения может существенно ускорить процесс поиска.

Путем разложения А = [B, N] матричное уравнение Ax = b представляется в виде

[B, N] (х^T_B, x^T_N)^T = b, (7)

или что эквивалентно,

Bх_B + Nx_N = b. (8)

Так как по определению матрица B имеет обратную матрицу, решение последнего уравнения относительно вектора х_B, получим в виде

х_B = B^-1 b - B^-1Nx_N. (9)

Принимая в этом выражении x_N = 0, получим базисное решение в виде

х_B = B^-1 b. (10)

Если оно неотрицательно, т.е. х_B ≥ 0, получим допустимое базисное решение. Этому решению соответствует вершина множества допустимых решений, которую можно определить в виде

х¹ = 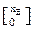. (11)