(симплекс - алгоритм )
В основе симплекс - метода решения задачи лежит итеративный процессе преобразования вершин области допустимых решений и проверки в них условия оптимальности. Вершины, как отмечалось выше, генерируются с помощью базисов. Табличный вариант алгоритма весьма удобен для машинного счета, так как связан с преобразованием таблиц – массивов данных, которые содержат сведения о текущем базисе, базисном решении, правиле остановки и, наконец, об оптимальном решении. В процессе преобразования таблиц, которое представляет собой реализацию процедуры полного исключения Гаусса, формируется также информация о двойственных переменных решаемой задачи.
Пусть задача представлена в канонической форме
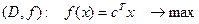 , (12)
, (12)
Ax = b
x ≥ 0.
где с и х – векторы размерности (п х1), т. е. сÎ Еп, хÎ Еп, А – матрица размерности (mхп), b – (пх1) – вектор.
Допустим, что матрица А допускает представление в виде А = [B, N], где B – (mхm) – матрица полного ранга. Для простоты предположим, что B - единичная матрица, т.е. B = I. Это может иметь место, например, если ограничения исходной задачи имеют вид Ax ≤ b. В случае неотрицательного вектора b, т. е. b ≥ 0, это предположение помогает найти первое базисное решение в виде
xB = B -!b = I -1b = b ≥ 0. (13)
Тогда первая вершина будет равна
х1 = (0Тп - m, bТ)Т, (14)
где через 0п–m обозначен нулевой вектор с п–m координатами. Для построения исходной таблицы обозначим через IB и IN, множества индексов векторов из B и N соответственно и вычислим так называемые симплекс -разности для векторов, принадлежащих N по формуле
(СР)j = cj – 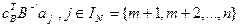 . (15)
. (15)
Симплекс – разности содержат в себе информацию об оптимальности текущего базисного решения, следовательно, и текущей вершины. Согласно этому правилу, если при решении задачи на максимум на каком-либо шаге (или итерации) симплексных преобразований имеет место
(СР)j £ 0, "j Î IN, (16)
тогда найденное базисное решение является оптимальным. В противном случае поиск решения продолжается.
Легко заметить, что для всех базисных векторов всегда имеет место условие
(СР)j = 0, "j Î IВ, (17)
т. е. векторы из В имеют нулевую симплекс – разность на всех этапах симплексных преобразований.
Рассмотрим для примера решение задачи
f(x) = 2 x 1 + 3 x 2 → max.
4 x 1 + 3 x 2 £ 12
x1 £ 2
x2 £ 3
x1, х2 ≥ 0
Удобно представить последующие действия в виде последовательности шагов алгоритма. Он состоит из предварительного и основного этапов.
Предварительный этап. Представить задачу в канонической форме
f(x) = 2x1 + 3x2 → max.
4x1 + 3x2 + x3 =12
x1 + x4 = 2
x2 + x5 = 3
xj ≥ 0, j = 1,…,5
Основной этап.
Шаг 1. Разложение матрицы А. Записать ограничения в виде матричного уравнения Ax = b, x ≥ 0, и представить матрицу А в виде
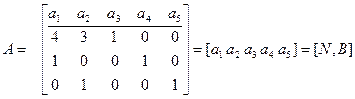 ,
,
выделив в ней (mxm) – матрицу B полного ранга. Удобно в данном случае выбрать в качестве начального базиса единичную матрицу B = [a3, a4, a5] = I, следовательно, N = [a1, a2], IB {3, 4, 5}, IN = {1, 2}. Как видно, B = I – единичная матрица размерности (3х3). Если получение базиса В не представляется возможным, то задача не имеет решения.
Шаг 2. Нахождение базисного решения. Начальному базису В соответствует базисное решение в виде
хB =(х3б, х4б, х5б)Т = B-1b = Ib = (12, 2, 3) Т.
Соответствующая этому базисному решению вершина равна х1 = (0, 0, 12, 2, 3)Т. Последние три координаты х1 совпадают ссоответствующими координатами хB, а первые две координаты равны нулю. Значение целевой функции в этой точке равно
f(x1) = f(xB) = cBTxВ = 0,
т.к. сВ =(с3, с4, с5)Т = (0, 0, 0)Т.
Шаг 3.Вычисление симплекс - разностей и построение правила остановки. Вычислим симплекс - разности для небазисных векторов из N. Так как IN = {1, 2}, имеем
(СР)1 = c1 – 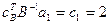 ,
,
(СР)2 = c2 – 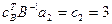 .
.
Легко заметить, что из-за нулевого вектора сВ = (0, 0, 0)Т имеет место условие
(СР)3 = (СР)4 = (СР)5 = 0.
Так как симплекс - разности (СР)1 и (СР)2 положительны, поиск оптимального решения продолжается.
Шаг 4.Построение и преобразование исходной таблицы Т0.
Исходная симплекс – таблица, соответствующая решаемой задаче, приведена на рис. 2.2.
исходная таблица Т0
|
|


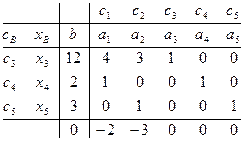
Рис. 2. Исходная симплекс – таблица.
Она содержит матрицу А, вектор b, базисное решение xB = b и так называемую индексную строку, в которой первый ее элемент – это текущее значение целевой функции f(x) = f(xB) = cBTxB, а остальные ее элементы – это так называемые индексы Dj = - (CP)j, j = 1, …, n, значение которых определяется как симплекс - разности с обратным знаком. Цифровая часть симплекс - таблицы называется ее главной частью: она и подвергается преобразованию от итерации к итерации.
Шаг 5. Проверка правила остановки
Если Dj ³ 0, j = 1, …, n, остановиться; найденное базисное решение является оптимальным, а значение целевой функции наибольшее. В данном случае обе величины Dj отрицательны. Это означает, что обе симплекс - разности (CP)j, j = 1, 2, положительные, следовательно, поиск продолжается.
Шаг 6. Выбор направляющего столбца и направляющей строки. Направляющий столбец с индексом j0 выбирается по наибольшему значению (CP)j > 0. В нашем случае это (CP)2 = 3, следовательно, j0 = 2. Направляющая строка с индексом i0 выбирается по правилу
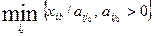 . (18)
. (18)
Согласно этому правилу, среди всех отношений типа 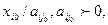 где xib – базисные переменные (их численные значения содержатся в столбце b),
где xib – базисные переменные (их численные значения содержатся в столбце b), 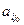 - положительные элементы направляющего столбца, выбирается наименьшее отношение с индексом i0. В нашем случае – это строка с индексом i0 = 5. Если в направляющем столбце положительных элементов нет, задача не имеет решения из-за неограниченности целевой функции.
- положительные элементы направляющего столбца, выбирается наименьшее отношение с индексом i0. В нашем случае – это строка с индексом i0 = 5. Если в направляющем столбце положительных элементов нет, задача не имеет решения из-за неограниченности целевой функции.
Выбору направляющей строки и направляющего столбца с индексами i0 и j0 соответственно соответствует исключение из базисного решения переменной 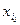 и включение вместо нее переменную
и включение вместо нее переменную 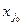 , причем, новой переменной в базисе присваивается значение
, причем, новой переменной в базисе присваивается значение
l0 = 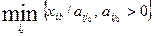 . (19)
. (19)
В текущей таблице элемент 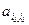 называется ведущим элементом и отмечается кружком.
называется ведущим элементом и отмечается кружком.
 2015-09-06
2015-09-06 1343
1343
