Математическая модель

Работа 1. Построение производственного

плана фирмы и его анализ

Постановка задачи и ее

математическая модель

Фирма планирует производство нескольких видов продукции, которые пользуются спросом на рынке. Известны рыночные цены на производимые товары, типы и объемы необходимых ресурсов (производственных факторов), а также технологические нормы использования ресурсов. Необходимо найти оптимальный план производства товаров (уровни или интенсивности производств), которые отвечают ограничениям задачи по ресурсам и максимизируют суммарный доход фирмы.

Для построения математической модели задачи введем следующие обозначения. Пусть x_j, j = 1,…, n, - искомые объемы производимых товаров; b_i, i = 1,…, m, - имеющиеся в распоряжении фирмы ресурсы (основные фонды, трудовые ресурсы и т.д.); а_ij, i = 1, …, m, j = 1, …, n, - технологические нормы расходования единиц ресурсов i – го типа на производство одной единицы продукции j – го типа; c_j, j = 1, …, n, - рыночные цены единиц продукций; f(x) – функция дохода фирмы от реализации продукций. Тогда математическая модель задачи состоит из элементов:

а) переменные задачи - x_j, j = 1,…, n, - искомые объемы производимых товаров;

б) ограничения задачи –

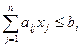, i = 1,…, m, x_j ≥ 0, j=1,…, n, (1)

в) целевая функция – функция дохода

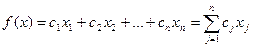. (2)

Цель фирмы заключается в нахождении таких объемов х₁^*, …, х_п^*, которые удовлетворяет ограничениям задачи и максимизирует функцию f(x). Искомое решение задачи обозначим вектором х^* = (х₁^*, …, х_п^*)^Т.

В наиболее общей форме математическая постановка этой задачи (задачи линейного программирования) имеет вид

(D, f): 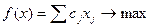, (3)

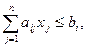i=1,…,m

x_j ≥ 0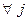

или в матричной форме

(D,f): 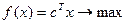, (4)

Ax ≤ b

x_j ≥ 0

где х = (х₁, …, х_п)^Т – вектор переменных задачи, f(x) целевая функция, D – множество допустимых решений. Целью задачи является нахождение такого вектора х^* из D, который максимизирует целевую функцию, т. е.

f(x^*) ³ f(x) " хÎ D. (5)

Задача (3) имеет ряд характерных особенностей (свойств), которые лежат в основе метода линейного программирования и соответствующего симплекс - алгоритма решения.

а) Множество допустимых решений D, если оно не пусто, то обязательно выпукло и либо ограничено (по расстоянию), либо не ограничено;

б) Множество D представляет собой многогранное множество (выпуклый многогранник), имеющее ограниченное число вершин, боковые ребра и боковые грани;

в) Линии уровня целевой функции, f(x) = const, представляют собой параллельные плоскости (или гиперплоскости), перпендикулярные направлению вектора коэффициентов с = (c₁, …, c_n)^T; направление этого вектора определяет направление возрастания значения целевой функции f(x), а его обратное направление – направление убывания значения f(x);

г) Если множество D ограничено, то целевая функция f(x) достигает на нем и своего максимального значения, и минимального значения как следствие центральной теоремы математического анализа – теоремы Вейерштрасса.

е) Если задача имеет оптимальное решение, то оно находится по крайней мере в одной из вершин множества D; задача может не иметь оптимального решения из-за неограниченности множества D, когда целевая функция на нем неограниченно возрастает или убывает;

ж) Алгоритм решения задачи представляет собой последовательность действий, связанных с генерацией вершин множества D и проверкой условия оптимальности (правила завершения работы).