Говорят, что две задачи линейного программирования находятся в отношении двойственности, если они имеют структуру
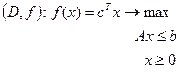 (21)
(21)
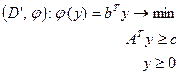 (22)
(22)
В них с, х Î Еп; y, b Î Еm; A – (mxn) – матрица, x, y ³ 0; D, D\ - области допустимых решений.
Как видно, в первой задаче, назовем ее прямой, целевую функцию необходимо максимизировать, а во второй задаче, назовем ее двойственной, она минимизируется; размерность первой задачи – (nxm), т. е. п переменных и m ограничений, а размерность второй задачи – (mxn), т. е. m переменных и п ограничений.
Наиболее важными свойствами двойственных задач являются:
а) 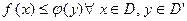 ; (23)
; (23)
б) если существуют векторы x* и y*, такие, что 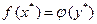 , то x* является оптимальным решением прямой, а y* – оптимальным решением двойственной задач;
, то x* является оптимальным решением прямой, а y* – оптимальным решением двойственной задач;
в) для оптимальных решений справедливы условия дополняюшей нежесткости Слейтера:
x*T(ATy* – c) = 0, (24)
y*T(- Ax* + b) = 0. (25)
Эти условия выражают «экономическую» сущность переменных: переменные хj, j = 1, …, n, являются «теневыми» ценами для второй задачи, а переменные yi, i = 1, …, m, - «теневыми» ценами для первой задачи. «Теневые» цены имеют важный экономический смысл. Они означают, что если какой либо ресурс bi в оптимальном плане использован не полностью, т.е. аix* < bi, то соответствующая двойственная переменная yi* равна нулю, т. е. имеет место
|
|
|
yi*(аix* - bi) = 0,, i = 1, …, m. (26)
Аналогично, если имеет место ajy* > cj, то соответствующая двойственная переменная xj* равна нулю, и должно выполняться условие
xj*(ajy* - cj) = 0. j = 1, …, n, (27)
В этих выражениях через aj обозначены строки матрицы А, а через aj – строки матрицы АТ.
г) оптимальные решения x* и y* связаны с соответствующими элементами индексной строки симплексных таблиц соотношениями
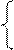
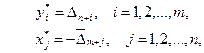 (28)
(28)
где 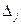 – элементы индексной строки прямой задачи,
– элементы индексной строки прямой задачи, 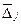 – элементы индексной строки двойственной задачи.
– элементы индексной строки двойственной задачи.
Например, в таблице T2 первой части работы имеем
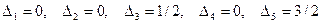 ,
,
следовательно,
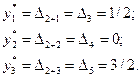
После решения двойственной задачи симплекс-методом, аналогичные соотношения находим и для двойственных переменных xj*, j = 1, …, n.
Иллюстрируем соотношения двойственности на уже рассмотренном выше примере.
Прямая задача:
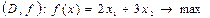
4x1 + 3x2 ≤ 12
x1 ≤ 2, x2 ≤ 3
x1, x2 ≥ 0
Двойственная задача:
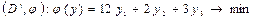 .
.
4y1 + 1y2 ≥ 2
3y1 + 1y3 ≥ 3
y1, y2, y3 ≥ 0
Оптимальные решения прямой и двойственной задачи имеют вид (смотри выше)
x0 = x* = (3/4, 3)T; y0 = y* = (1/2, 0, 3/2)T,
f (x0) = 21/2 = 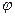 (y0) = 21/2.
(y0) = 21/2.
Эти решения удовлетворяют условиям дополняющей нежесткости Слейтера:
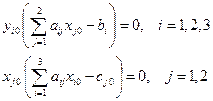
 2015-09-06
2015-09-06 215
215








