Тень овоида, эллипсоида, параболоида

Тень овоида, эллипсоида, параболоидаи т. д. можно по­строить, исходя из одной проекции, методом описанных или вписан­ных (касательных), конусов, цилиндров и шаров, т. е. тем методом, который показан (рис. 6).

Обратимся к примеру рис. 23, на которой построены собствен­ная тень поверхности вращения яйцевидной формы (будем ее называть овоидом) и тень, падающая от нее на плоскость V, в предпо­ложении, что ось поверхности отстоит от V на расстоянии Y_о.

Видно, что точки а' и e' собственной тени, лежащие на экваторе, найдены как точки, через которые проходят теневые образующие описанного вертикального цилиндра.

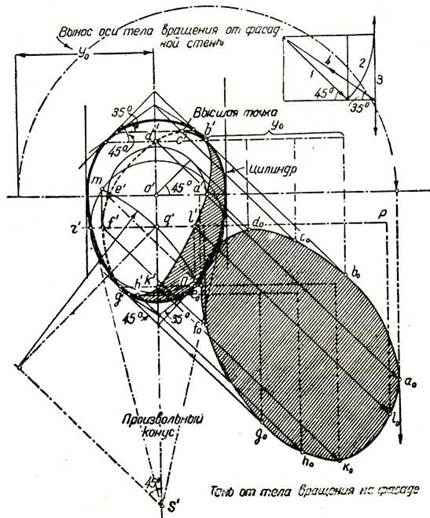Рис. 23

Точки b' и g' на фронтальном меридиане, а также и точки d' и k' на профильном меридиане найдены как точки касания к поверхности вращения теневых образующих описанных конусов с образующей под углом 45° к основанию (см. также рис. 18, г).

Точки с' и h' — наивысшая и низшая — найдены как точки касания к поверхности теневых образующих касательных ко­нусов собразующей под углом 35° к основанию (см. также рис. 18, б). Наконец, случайные точки контура l' и f' найдены на произвольной параллели r'q' как точки касания к поверхности тене­вых образующих конуса S, касающегося к поверхности по взятой параллели (см. также рис. 18, д).

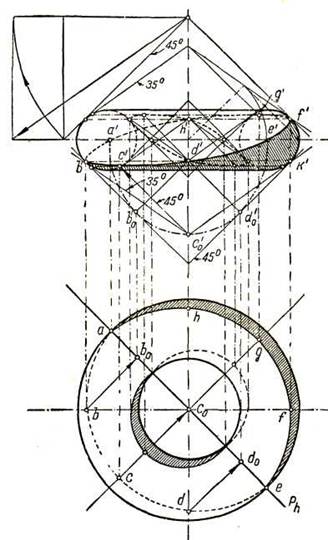Рис. 24

В том случае, когда вершина S вспомогательного конуса уходит за пределы чертежа, можно заменить конус вписанной сферой, касающейся поверхности вра­щения по параллели q'r'. Центр такой сферы будет лежать на пересечении с осью q'k' нормали к очерку в точке r'. Точки l' и f' найдутся как точки пересе­чения с параллелью контура собственной тени шара.

Контур падающей тени найден после нахождения теней, падающих на V от отдельных точек собствен­ной тени, путем откладыва­ния выноса соответствую­щей точки (ее ординаты) сначала вправо по горизон­тали от вертикальной про­екции точки, а затем вниз по вертикали.

При этом ординаты точек, располо­женных на экваторе и на фронтальном и профильном меридианах, а так кг и выс­шей и низ л ей точек полу­чаются непосредственно пу­тем прибавления к орди­нате Y_о или вычитания из нее расстояний этих точек от оси поверхности враще­ния, видимых на проекции; ордината случайной точки l' получается от прибавления к Y_o полухорды l'n, а ордината точки f' —путем вычитания из Y_o этой же полухорды.

Направление в 35° к горизонту для построения касательных ко­нусов с таким наклоном образующей к основанию может быть опре­делено без транспортира путем построения угла, тангенс которого равен 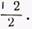Построение такого угла показано на рис. 23 в выноске вверху справа и понятно из чертежа, так как на последнем указана стрелками и номерами последовательность проведения линий.