|
Определение. Группой 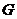 называется непустое множество, в котором для любых двух элементов называется непустое множество, в котором для любых двух элементов 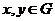 определен элемент определен элемент 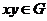 (произведение), причем: (произведение), причем:
1) 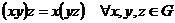 ; ;
2) 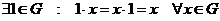 ; ;
3) 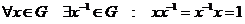 . . Примеры групп:
1) 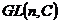 - невырожденные матрицы размера - невырожденные матрицы размера 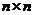 с комплексными коэффициентами – группа относительно операции умножения матриц; с комплексными коэффициентами – группа относительно операции умножения матриц;
2) 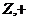 - целые числа – группа относительно операции сложения целых чисел; - целые числа – группа относительно операции сложения целых чисел;
3) Группа диэдра 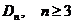 : :
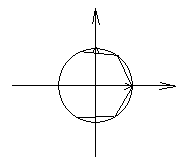 Рассмотрим на плоскости ортонормированный базис, приведем окружность единичного радиуса с центром в начале координат. Впишем в нее правильный Рассмотрим на плоскости ортонормированный базис, приведем окружность единичного радиуса с центром в начале координат. Впишем в нее правильный 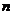 -угольник, одна из вершин которого находится в конце вектора -угольник, одна из вершин которого находится в конце вектора 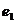 . . 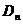 - это все движения плоскости, переводящие этот - это все движения плоскости, переводящие этот 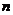 -угольник в себя. -угольник в себя.
Убедимся в том, что это множество будет группой относительно композиции движений:
1) композиция движений ассоциативна;
2) в качестве единичного элемента можно взять тождественное движение;
3) в качестве обратного элемента можно взять обратное движение.
Рассмотрим эту группу более подробно. При любом таком движении центр 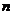 -угольника остается на месте, следовательно, это ортогональное преобразование плоскости, т.е. либо поворот на некоторый угол, либо симметрия относительно некоторой прямой. -угольника остается на месте, следовательно, это ортогональное преобразование плоскости, т.е. либо поворот на некоторый угол, либо симметрия относительно некоторой прямой.
Т.к. при повороте вершина 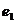 должна перейти в какую-то вершину, то поворот может быть только на угол должна перейти в какую-то вершину, то поворот может быть только на угол 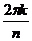 , где , где 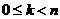 . Обозначим матицу поворота на угол . Обозначим матицу поворота на угол 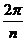 за за 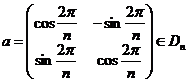 . В качестве симметрии подходит, например, симметрия относительно оси . В качестве симметрии подходит, например, симметрия относительно оси 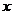 , матрица такого преобразования , матрица такого преобразования 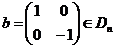 . .
Теорема. Группа 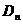 состоит из состоит из 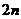 элементов, а именно элементов, а именно 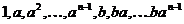 и и 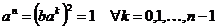 . . Доказательство.
Как уже говорилось, поворот может быть только на угол 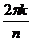 , где , где 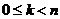 . Запишем матрицу такого поворота: . Запишем матрицу такого поворота: 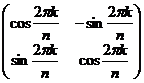 , но ни что иное как , но ни что иное как 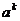 . Следовательно . Следовательно 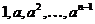 - это все повороты, входящие в группу - это все повороты, входящие в группу 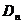 . .
Пусть теперь 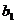 - это какая-нибудь симметрия из группы - это какая-нибудь симметрия из группы 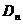 . Тогда . Тогда 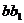 тоже принадлежит этой группе, причем это ортогональная матрица и ее определитель равен тоже принадлежит этой группе, причем это ортогональная матрица и ее определитель равен  . Следовательно, это поворот, т.е. . Следовательно, это поворот, т.е. 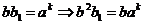 . Т.к. . Т.к. 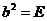 , то , то 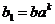 , следовательно, все симметрии из , следовательно, все симметрии из 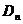 - это - это 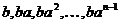 . .
Мы доказали, что группа 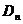 не содержит ничего кроме элементов не содержит ничего кроме элементов 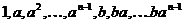 , докажем теперь, что все эти элементы различны. Все элементы , докажем теперь, что все эти элементы различны. Все элементы 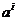 различны, т.к. это повороты на разные углы. Если различны, т.к. это повороты на разные углы. Если 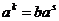 , то , то 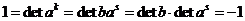 , что невозможно. Если , что невозможно. Если 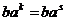 , то , то 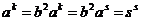 , а мы уже доказали, что это невозможно. , а мы уже доказали, что это невозможно.
И последнее утверждение теоремы. 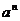 - это поворот на угол - это поворот на угол 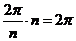 , т.е. тождественное движение. Т.к. , т.е. тождественное движение. Т.к. 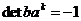 , то это симметрия относительно некоторой прямой, но симметрия в квадрате это всегда тождественное движение, следовательно, , то это симметрия относительно некоторой прямой, но симметрия в квадрате это всегда тождественное движение, следовательно, 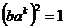 . .  Упражнение. Доказать, что 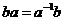 . . 4) приведем пример еще одной группы – группы кватернионов 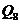 . Рассмотрим матрицы . Рассмотрим матрицы 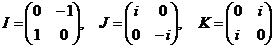 . . Упражнение. Доказать, что 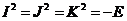 , , 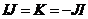 , , 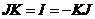 , , 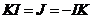 . Доказать, что матрицы . Доказать, что матрицы 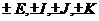 образуют группу относительно операции умножения матриц. образуют группу относительно операции умножения матриц. Упражнение. Докажите, что в любой группе единичный элемент 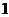 определен однозначно и для любого элемента определен однозначно и для любого элемента 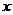 обратный элемент обратный элемент 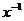 также определен однозначно. также определен однозначно. Определение. Порядком группы 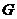 называется количество элементов в группе, обозначается называется количество элементов в группе, обозначается 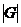 . . Упражнение. Рассмотрим группу 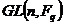 - невырожденные матрицы - невырожденные матрицы 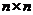 над полем из над полем из 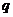 элементов. Доказать, что ее порядок равен элементов. Доказать, что ее порядок равен 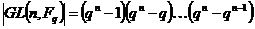 . . Определение. Пусть 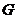 - группа. Непустое подмножество - группа. Непустое подмножество 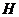 в в 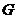 называется подгруппой, если 1) называется подгруппой, если 1) 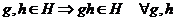 ; ;
2) 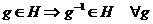 . . Замечание. Единичный элемент всегда принадлежит любой подгруппе. Т.к. 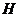 непустое, то там есть хотя бы один элемент непустое, то там есть хотя бы один элемент 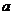 . По свойству 2) . По свойству 2) 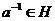 , по свойству 1) , по свойству 1) 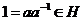 . . Упражнение. Докажите, что в любой группе пересечение любого числа подгрупп тоже будет подгруппой. Примеры подгрупп:
1) Группа 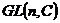 . Ее подгруппы: . Ее подгруппы: 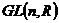 ; ; 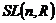 - вещественные матрицы с определителем единица; - вещественные матрицы с определителем единица; 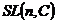 ; ; 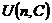 - унитарные матрицы; - унитарные матрицы; 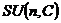 - унитарные матрицы с определителем единица; - унитарные матрицы с определителем единица; 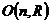 - ортогональные матрицы; - ортогональные матрицы; 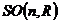 ; ( ; (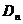 ; ; 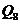 - подгруппы в группе - подгруппы в группе 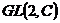 ); );
2) 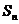 - группа подстановок. - группа подстановок. 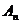 (четные подстановки) – подгруппа. В частном случае, если (четные подстановки) – подгруппа. В частном случае, если 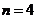 множество множество 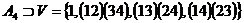 также будет подгруппой; также будет подгруппой;
3) 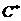 - группа ненулевых комплексных чисел относительно умножения. Ее подгруппы: - группа ненулевых комплексных чисел относительно умножения. Ее подгруппы: 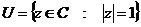 - единичная окружность; - единичная окружность; 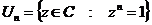 - корни из единицы. - корни из единицы. Определение. Пусть 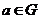 - элемент группы и - элемент группы и 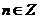 - целое число, тогда - целое число, тогда 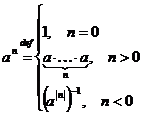 . . Теорема. Если 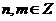 , то , то 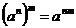 и и 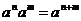 . . Упражнение. Докажите теорему. Определение. Пусть 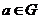 . Порядком элемента . Порядком элемента 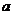 (обозначается (обозначается 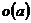 или или 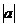 ) называется наименьшее натуральное ) называется наименьшее натуральное 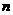 такое, что такое, что 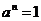 . Если такого числа не существует, то элемент имеет бесконечный порядок. . Если такого числа не существует, то элемент имеет бесконечный порядок. Упражнение. Найдите порядок элемента 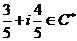 . . Предложение. Пусть 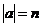 . Для целого числа . Для целого числа 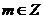 следующие условия эквивалентны: следующие условия эквивалентны:
1) 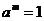 ; ;
2) 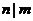 . .
Доказательство.
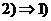 . Пусть . Пусть 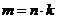 , , 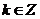 , тогда , тогда 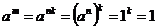 . .
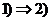 . Пусть . Пусть 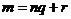 , где , где 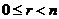 , тогда , тогда 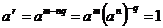 . Следовательно . Следовательно 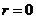 , т.к. иначе имели бы , т.к. иначе имели бы 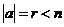 . Следовательно . Следовательно 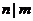 . . 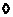 . .
|

