|
Определение. Алгебра с умножением  называется алгеброй Ли, если это умножение не ассоциативно, антикоммутативно и выполняется тождество называется алгеброй Ли, если это умножение не ассоциативно, антикоммутативно и выполняется тождество 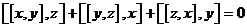 . .
Примеры:
1) Пусть 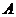 - ассоциативная алгебра с умножением - ассоциативная алгебра с умножением  , тогда введем умножение , тогда введем умножение 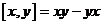 . Относительно этого нового умножения наша алгебра будет алгеброй Ли. . Относительно этого нового умножения наша алгебра будет алгеброй Ли.
2)  - множество матриц размера - множество матриц размера 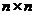 над полем над полем 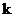 со следом ноль. Операция умножения со следом ноль. Операция умножения  , где , где  - обычное матричное умножение. - обычное матричное умножение.
3) 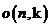 - множество кососимметричных матриц. Умножение - множество кососимметричных матриц. Умножение  . .
4)  , операция умножения - векторное произведение , операция умножения - векторное произведение 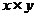 . .
Определение. Пусть  - алгебра. Дифференцированием на - алгебра. Дифференцированием на  называется линейный оператор называется линейный оператор  , такой что , такой что 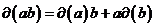 . .
Упражнение. Если 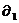 и и  - дифференцирования в алгебре - дифференцирования в алгебре 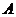 , то их коммутатор , то их коммутатор 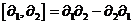 - снова дифференцирование. И все дифференцирования образуют алгебру Ли. - снова дифференцирование. И все дифференцирования образуют алгебру Ли.
Рассмотрим алгебру Ли 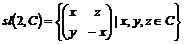 , построим в ней базис: , построим в ней базис: 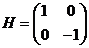 , , 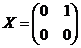 и и 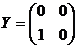 . .
Упражнение. Докажите, что 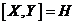 , , 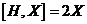 , ,  . .
Теорема. Алгебра Ли 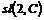 проста. проста.
Доказательство.
Пусть 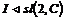 - ненулевой идеал, и пусть - ненулевой идеал, и пусть  - ненулевой элемент. - ненулевой элемент.
1) Если  , тогда , тогда 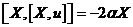 . Следовательно, . Следовательно, 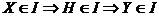 и и  . .
2) Если 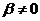 , то , то 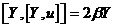 , далее аналогично получаем, что , далее аналогично получаем, что 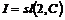 . .
3) Если 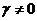 и и 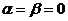 , то , то 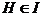 , а, следовательно, и , а, следовательно, и  . И опять . И опять 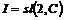 . . 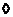
Упражнение. 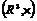 - простая алгебра Ли. - простая алгебра Ли.
| 









