Энергия сольватации представляет собой выигрыш в энергии, который получается при перенесении моля исследуемых ионов из ваку-ума в данный растворитель. При этом предпо-лагается, что такой выигрыш энергии не вклю-чает в себя электростатическое взаимодействие ионов, которое неизбежно сказалось бы уже при введении в растворитель второго и каждого по-следующего ионов. Чтобы избежать этого ослож-нения, раствор нужно поддерживать электроней-тральным, т.е. вводить в него соответствующее количество ионов противоположного знака, а взаимное притяжение катионов и анионов элими-нировать (исключать, устранять) достаточным (теоретически бесконечным) разбавлением раствора.
Наиболее простая модель для оценки энергии сольватации была предложена М. Борном. Сог-ласно этой модели, ион рассматривается как заряженный шарик радиуса 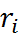 , а растворитель – как сплошная однородная среда (континуум) с диэлектрической постоянной
, а растворитель – как сплошная однородная среда (континуум) с диэлектрической постоянной 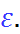 Процесс перено-са заряженного шарика из вакуума в среду разбивается на три этапа: 1) разряд шарика в вакууме; 2) перенос незаряженного шарика из вакуума в растворитель; 3) заряжение шарика в среде (рис. 2.2).
Процесс перено-са заряженного шарика из вакуума в среду разбивается на три этапа: 1) разряд шарика в вакууме; 2) перенос незаряженного шарика из вакуума в растворитель; 3) заряжение шарика в среде (рис. 2.2).
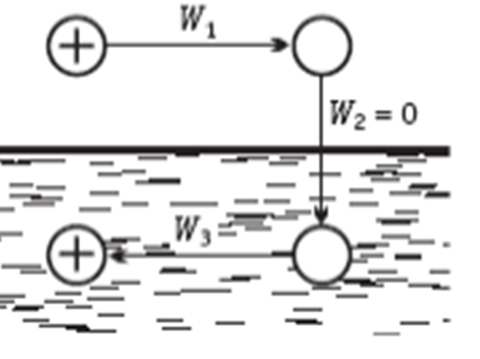
Рис. 2.2. Схема для расчета энергии
сольватации иона по модели Борна
При этом предполагается, что работа на втором
этапе 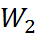 = 0, а для расчета работы на этапах 1 и 3 (
= 0, а для расчета работы на этапах 1 и 3 (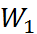 и
и 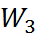 ) используются основные законы эле-ктростатики. Так, согласно закону Кулона, сила, действующая на каждый из двух зарядов
) используются основные законы эле-ктростатики. Так, согласно закону Кулона, сила, действующая на каждый из двух зарядов 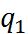 и
и 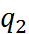 (с учетом знака), находящихся в среде с диэлектрической постоянной
(с учетом знака), находящихся в среде с диэлектрической постоянной 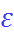 на расстоянии r, равна:
на расстоянии r, равна:
F = 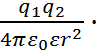 (2.3.1)
(2.3.1)
Поэтому напряженность поля X, т.е. сила, которая действует на заряд +1, находящийся на расстоянии r от заряда q, составляет:
X = 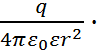 (2.3.2)
(2.3.2)
Поскольку напряженность поля связана с электрическим потенциалом 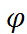 общей формулой X =
общей формулой X = 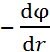 , то для потенциала на поверхности сферы радиуса
, то для потенциала на поверхности сферы радиуса 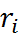 получаем:
получаем:
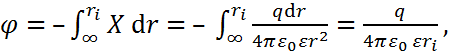 (2.3.3)
(2.3.3)
где нижний предел интегрирования соответст-вует выбору нулевого потенциала на бесконечно большом расстоянии от рассматриваемой сферы. Из уравнения (2.3.3) вытекает следующая формула для работы заряжения сферы:
W = 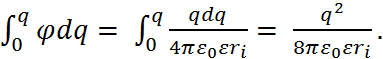 (2.3.4)
(2.3.4)
В соответствии с формулой (2.3.4), для ра-бот 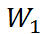 и
и 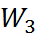 получаем выражения
получаем выражения
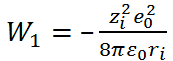 и
и 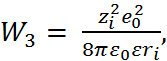
где 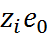 – заряд иона.
– заряд иона.
Учитывая, что свободная энергия сольвата-ции 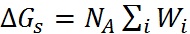 , выводим основную формулу модели Борна:
, выводим основную формулу модели Борна:
– 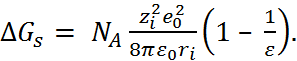 (2.3.5)
(2.3.5)
Если воспользоваться уравнением Гиббса-Гельмгольца, согласно которому
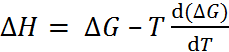 , (2.3.6)
, (2.3.6)
то из уравнения (2.3.5) можно получить также выражение для энергии сольватации:
– 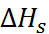 =
= 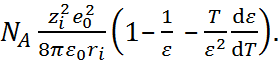 (2.3.7)
(2.3.7)
Уравнение (2.3.7) называют уравнением Борна – Бьеррума. Результаты расчета по формулам (2.3.5) и (2.3.7) для гидратации катионов щелочных металлов и анионов галогенов представлены в табл. 2.2
Энергии гидратации, рассчитанные по модели Борна, весьма значительны и достаточны для разрушения для кристаллической решётки при образовании растворов электролитов. Этот наиболее важный качественный вывод из теории Борна показывает, что основной причиной обра-
зования и устойчивости растворов электролитов служит сольватация ионов. К этому выводу можно прийти также, не производя расчетов, а сопоставляя формулы (2.2.6) и (2.3.5). Если в этих формулах пренебречь 1/ n и 1/ 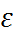 по сравнению с единицей, положить
по сравнению с единицей, положить 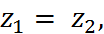
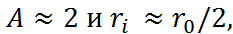 то энергия сольватации одного иона окажется равной половине энергии кристаллической решётки. Иначе говоря, энергия сольватации двух ионов – катиона и аниона – как раз скомпенсирует энергию разрушения решетки кристалла.
то энергия сольватации одного иона окажется равной половине энергии кристаллической решётки. Иначе говоря, энергия сольватации двух ионов – катиона и аниона – как раз скомпенсирует энергию разрушения решетки кристалла.
Для количественной проверки теории сольва-тации Борна удобно воспользоваться следующим приёмом. Сложим энтальпии гидратации катиона и аниона, приведенные в табл. 2.2, и сравним полученную величину с тепловым эффектом сольватации соответствующей соли, вычислен-ным из термодинамического цикла. Например, для хлорида натрия
Таблица 2.2. Свободные энергии Гиббса и энтальпии гидратации, рассчитанные по модели Борна при 25 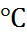
| Ион | 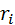 (по Полингу), нм (по Полингу), нм | – 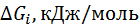 | – 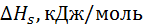 |
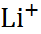 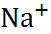 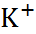 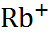 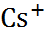 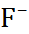 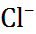 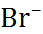 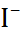 | 0,060 0,095 0,133 0,148 0,169 0,136 0,181 0,195 0,216 |
 NaC
NaC 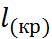
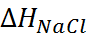 N
N 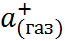 + С
+ С 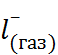
 |  | ||
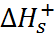
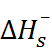
– 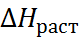
N 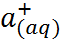 + C
+ C 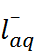
__________________
где 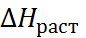 – тепловой эффект растворения, экстраполированный на бесконечно разбавлен-ный раствор соли.
– тепловой эффект растворения, экстраполированный на бесконечно разбавлен-ный раствор соли.
Из этого цикла для теплового эффекта сольватации хлорида натрия получаем:
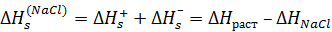 =4 – 772= –768кДж/моль.
=4 – 772= –768кДж/моль.
Аналогичным способом можно рассчитать 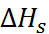 и для других солей. Экспериментальные и рассчитанные по Борну величины
и для других солей. Экспериментальные и рассчитанные по Борну величины 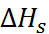 для хло-ридов щелочных металлов сопоставлены в табл. 2.3.
для хло-ридов щелочных металлов сопоставлены в табл. 2.3.
Рассчитанные по Борну величины 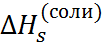 значительно превышают соответствующие экс-периментальные значения. Это указывает на весьма приближенный характер допущений, положенный в основу модели Борна. Поэтому были предприняты неоднократные попытки уточнить теорию сольватации Борна (Бернал и Фаулер; Уэбб; ван-Аркель и де-Бур; Эли и Эванс; Френк и Венн и др.). Некоторые из них проводились в рамках все того же контину-ального подхода (например, поправки на умень-шение диэлектрической постоянной раствори-теля вблизи иона за счет более жесткой ориентации диполей в поле иона, а также учет работы сжатия растворителя при введении в него электролита – эффекта электрострикции).
значительно превышают соответствующие экс-периментальные значения. Это указывает на весьма приближенный характер допущений, положенный в основу модели Борна. Поэтому были предприняты неоднократные попытки уточнить теорию сольватации Борна (Бернал и Фаулер; Уэбб; ван-Аркель и де-Бур; Эли и Эванс; Френк и Венн и др.). Некоторые из них проводились в рамках все того же контину-ального подхода (например, поправки на умень-шение диэлектрической постоянной раствори-теля вблизи иона за счет более жесткой ориентации диполей в поле иона, а также учет работы сжатия растворителя при введении в него электролита – эффекта электрострикции).
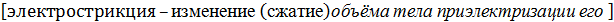
Таблица 2.3. 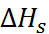 при гидратации хлоридов щелочных металлов при 25
при гидратации хлоридов щелочных металлов при 25 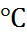
| Способ расчета | 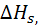 кДж/моль кДж/моль | ||||
| LiCl | NaCl | KCl | RbCl | CsCl | |
| Из термодинамического цикла | –883 | –768 | –685 | –664 | –639 |
| По модели Борна | –1549 | –1121 | –911 | –857 | –799 |
Предлагались также поправки, основанные на учете реальных микроскопических свойств дипольных жидкостей, например тетраэдриче-ской структуры воды и энергии её разрушения в ходе сольватации. Детализация микроскопиче-ского строения растворов, развитие молекуляр-но-статистических теорий и расчетных методов позволяют в настоящее время использовать значительно более сложные модели и во многих случаях устранить различия между рассчитанны-ми и экспериментальными значениями 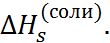 Однако при детальной проверке этих моделей встает задача экспериментального определения энергии сольватации отдельного иона, так как при суммировании рассчитанных величин
Однако при детальной проверке этих моделей встает задача экспериментального определения энергии сольватации отдельного иона, так как при суммировании рассчитанных величин 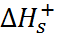 и
и 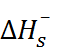 ошибки, обусловленные недостатками моде-лей, могут скомпенсироваться.
ошибки, обусловленные недостатками моде-лей, могут скомпенсироваться.
 2015-05-26
2015-05-26 8678
8678








