Свойства логарифмической функции с основанием большим единицы

· Область определения: 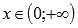. При х стремящемся к нулю справа, значения функции стремятся к минус бесконечности.

· Областю значений логарифмической функции является все множество действительных чисел, то есть, интервал .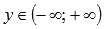

· Функция не является ни четной, ни нечетной, то есть она общего вида.

· Функция возрастает при .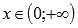

· Функция выпуклая при .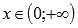

· Точек перегиба нет.

· Горизонтальных асимптот нет.

· Функция проходит через точку (1;0).

25. Непрерывность функции в точке. Примеры. Разрывная функция. Примеры

Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.

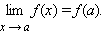
Разрывная функция – функция, не являющаяся непрерывной хотя бы в одной точке области определения.

y=cos (1: х) разрывна в точке x=0

26. Свойства непрерывных функций.

· Сумма непрерывных функций есть функция непрерывная.

· Произведение непрерывных функций есть функция непрерывная.

· Частное от деления непрерывных функций есть функция непрерывная – за исключением точек, в которых знаменатель обращается в нуль.

· Любая элементарная функция непрерывна в области своего определения

· Пусть функция непрерывна на промежутке [a,b] и принимает на его концах значения разных знаков. Тогда на этом промежутке существует такая точка c, в которой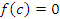

27. Непрерывность элементарных функций.

· Целая и дробная рациональные функции. Непрерывность f(x)=const и f(x)=x

· Показательная функция y=a^x(a>1) монотонно возрастает на всем интервале 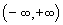. Ее значения заполняют весь интервал .

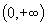· Логарифмическая функция 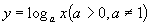. Рассмотрим случай a>1. Эта функция возрастает при 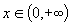, и принимает любое значение из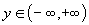

· Степенная функция 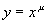. При возрастании x от 0 до 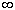возрастает 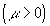или убывает 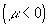на интервале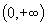

· Тригонометрические функции

· Обратные тригонометрические функции

28. Точки разрыва и их классификация.

Точка х₀ называется точкой разрыва функции f(x), если f(x) не определена в точке х₀ или не является непрерывной в этой точке.

· Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.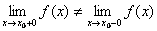

· Точка х₀ называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен.

29. Непрерывность функции на интервале и на отрезке

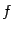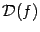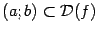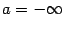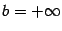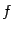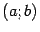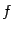Пусть - некоторая функция - её область определения и - некоторый (открытый) интервал (может быть с и/или ). Назовём функцию непрерывной на интервале если непрерывна в любой точке 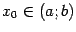то есть для любого 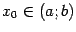существует 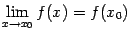(в сокращённой записи:

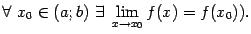
Пусть теперь 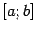- (замкнутый) отрезок в 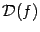. Назовём функцию 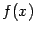непрерывной на отрезке 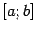, если 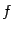непрерывна на интервале 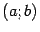, непрерывна справа в точке 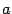и непрерывна слева в точке 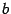, то есть

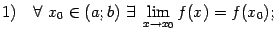
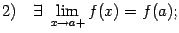
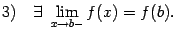
30. Свойства функций непрерывных на отрезке.

Функцию f(x) называют непрерывной на отрезке [ а, b ], если она непрерывна в каждой точке интервала (а, Ь).

а) Функция, непрерывная на отрезке [a, b], принимает на нем наибольшее и наименьшее значения.

б) Функция, непрерывная на отрезке, ограничена на этом отрезке

в) Функция, непрерывная на отрезке [a, b], принимает на этом отрезке все значения между двумя произвольными величинами

г) Если функция f(x) непрерывна в точке х = х₀, то существует некоторая окрестность точки х₀, в которой функция сохраняет знак.

д) Если функция f(x)- непрерывная на отрезке [a, b] и имеет на концах отрезка значения противоположных знаков, то существует такая точка внутри этого отрезка, где f(x) = 0

е) Функция, непрерывная на отрезке, равномерно непрерывна на нем

ж) Если функция f(x) определена, монотонна и непрерывна на некотором промежутке, то и обратная ей функция х = g(y) тоже однозначна, монотонна и непрерывна.

31. Производная функции, ее геометрический и экономический смысл.

Производная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если таковой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Процесс вычисления производной называется дифференци́рованием. Обратный процесс — интегрирование.

Геометрический смысл производной. Производная в точке x ₀ равна угловому коэффициенту касательной к графику функции y = f (x) в этой точке.

Экономический смысл производной: производная выступает как интенсивность изменения некоторого экономического объекта (процесса) по времени или относительно другого исследуемого фактора.

32. Уравнение касательной к кривой. Уравнение нормали к кривой

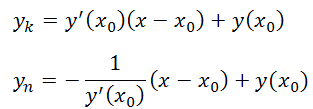
33. Односторонние производные функции в точке.

Правой (левой) производной функции f(x) в точке х = х₀ называется правое (левое) значение предела отношения 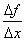при условии, что это отношение существует.

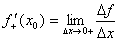
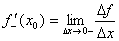
Если функция f(x) имеет производную в некоторой точке х = х₀, то она имеет в этой точке односторонние производные.

34. Основные правила дифференцирования

Обозначим f(x) = u, g(x) = v - функции, дифференцируемые в точке х.

1) (u ± v)¢ = u¢ ± v¢

2) (u×v)¢ = u×v¢ + u¢×v

3) 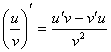, если v ¹ 0

35. Производная сложной функции.

Пусть y = f(x); u = g(x), причем область значений функции u входит в область определения функции f.

Тогда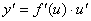

36. Производная функции, заданной параметрически.

Пусть задана зависимость двух переменных x и y от параметра 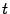, изменяющегося в пределах от α до β:

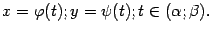
Пусть функция x = φ (t) имеет обратную: 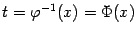. Тогда мы можем, взяв функци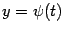и и 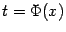, получить зависимость y от x: 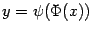. Зависимость величины y от величины x, заданная через зависимость каждой из них от параметра 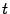в виде 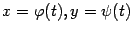, называется функцией y = y (x), заданной параметрически.

37. Производная функции, заданной в неявном виде.

Если y = f (x) - дифференцируемая функция, заданная уравнением F (x, y) = 0, т. е. F (x, f (x)) ≡ 0 на некотором интервале [ a, b ], то во многих случаях ее производную можно найти из уравнения

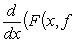
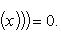
38. Логарифмическое дифференцирование.

Функция вида y =[ u (x)] ^{v (x)} называется степенно – показательной. Для вычисления ее производной (при условии, что у' существует), нужно прологарифмировать функцию по любому основанию (обычно по основанию). Затем нужно вычислить производную полученной неявной функции.

Логарифмическим дифференцированием называется метод дифференцирования функций, при котором сначала находится логарифм функции, а затем вычисляется производная от него.

Логарифмической производной функции y=f(x) называется производная от логарифма этой функции, т.е.

(ln f(x))'=f'(x)/f(x)

39. Производная обратных функций.

Пусть функция 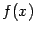имеет в точке 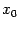производную 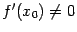. Тогда обратная функция 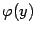имеет в соответствующей точке 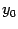производную 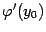, которую можно отыскать по формуле

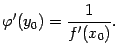
40. Дифференциал функции. Геометрический смысл дифференциала. Свойства дифференциала. Линеаризация функции. Применение дифференциала к приближенным вычислениям.

Дифференциалом функции называется линейная относительно 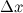часть приращения функции. Она обозначается как 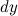или 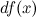. Таким образом:

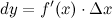
Геометрический смысл дифференциала

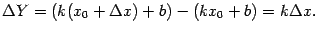
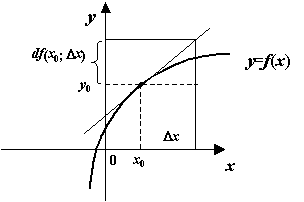
Свойства:

1. Дифференциал постоянной равен нулю

2. Дифференциал суммы дифференцируемых функций равен сумме дифференциалов слагаемых:

d(u+v)=du + dv

3. Дифференциал произведения двух дифференцируемых функций равен произведению первой функции на дифференциал второй плюс произведение второй на дифференциал первой:

d(uv) = udv + vdu.

4. Дифференциал частного u/v двух дифференцируемых функций и = и(х) и v = v(x) определяется формулой

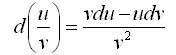
5. Свойство независимости вида дифференциала от выбора независимой переменной: дифференциал функции равен произведению производной на дифференциал аргумента независимого от того, является ли этот

аргумент независимой переменной или функцией другой независимой переменной.

Линеаризация функций применяется для нахождения пределов в точке, при построении графиков функций, для решения уравнений. Суть метода состоит в том, что в окрестности какой-либо точки, в которой функция f (x) непрерывна и дифференцируема нужное количество раз, ее можно заменить ее касательной f (x ₀) + f' (x ₀) · (x – x ₀). Чем ближе к x ₀ находится точка x, тем больше точность данного приближения.