Формула Тейлора

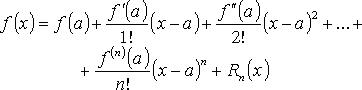
(R_n(x) - остаточный член формулы Тейлора).

Остаточный член в форме Лагранжа:

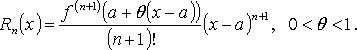
Формула конечных приращений или теорема Лагранжа о среднем значении утверждает, что если функция 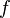непрерывна на отрезке 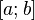и дифференцируема в интервале 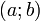, то найдётся такая точка 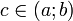, что

.

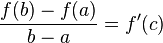43. Формула Маклорена.

Пусть функция f(x)имеет производную в точке x=0. Тогда в некоторой окрестности этой точки функцию f(x) можно представить в виде

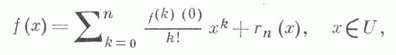
где r _п (х) - остаточный член n-го порядка, представимый в том или ином виде.

44. Представление некоторых элементарных функций по формуле Тейлора. Главная часть функции, выделение главной части.

а) Рассмотрим функцию 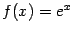. Все её производные совпадают с ней: 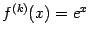, так что коэффициенты Тейлора в точке 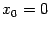равны

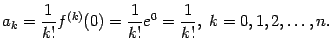
Поэтому формула Тейлора такова:

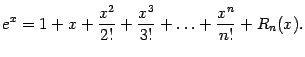
б) Рассмотрим функцию 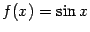. Её производные чередуются в таком порядке:

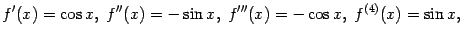
а затем цикл повторяется. Поэтому при подстановке 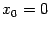также возникает повторение:

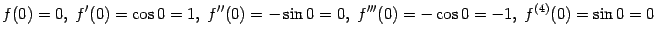
Получаем формулу Тейлора для синуса:

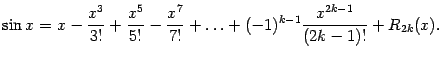
в) Для функции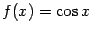

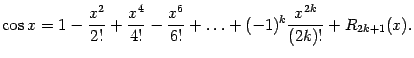
45. Теорема Ферма. Теорема Ролля. Теорема Лагранжа. Формула конечных приращений или формула Лагранжа. Теорема Коши

Теорема Ферма:

Для любого натурального числа 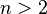уравнение

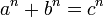
не имеет натуральных решени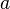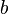й , и .

Теорема Ролля:

Пусть функция 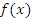дифференцируема в открытом промежутке 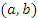, на концах этого промежутка сохраняет непрерывность и принимает одинаковые значения: 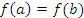. Тогда существует точка 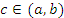, в которой производная функции 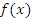равна нулю: .

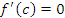Теорема Лагранжа:

Пусть функция 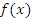дифференцируема в открытом промежутке 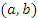и сохраняет непрерывность на концах этого промежутка. Тогда существует такая точка 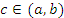, что

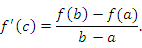
Теорема Коши:

Пусть функции y = f(x), y = g(x) непрерывны на отрезке и дифференцируемы на интервале (a, b), причем g ' (x) ≠ 0 на (a, b).

Тогда существует число c (a,b) такое, что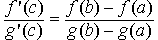

46. Правило Лопиталя

Пусть при x 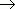a для функций f (x) и g (x), дифференцируемых в некоторой окрестности точки а, выполняются условия:

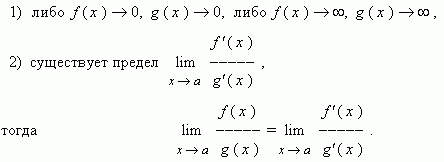
47. Производные и дифференциалы высших порядков. Общие правила нахождения высших производных. Второе достаточное условие экстремума