Преобразование сдвига

Tx,Ty - величина сдвига по осям, а матрица Т имеет вид:

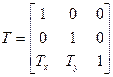
Преобразование зеркальное отображение:

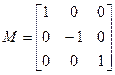
Замечание: следует помнить, что результат преобразования зависит от порядка выполнения операций. Свойством мультипликативности обладают только матрицы [D] и [M].

Однородные координаты - мощный математический инструмент, находящий свое применение в различных разделах компьютерной графики - геометрическом моделировании, визуализации, машинном зрении и т.д. Однородные координаты явно или неявно используются в любом графическом пакете на этапах преобразования и затенения геометрии, например, в OpenGL или DirectX

Однородные координаты - это математический механизм, связанный с определением положения точек в пространстве. Привычный аппарат декартовых координат, не подходит для решения некоторых важных задач в силу следующих соображений:

• В декартовых координатах невозможно описать бесконечно удаленную точку. А многие математические и геометрические концепции значительно упрощаются, если в них используется понятие бесконечности. Например, "бесконечно удаленный источник света".
• С точки зрения алгебраических операций, декартовы координаты не позволяют провести различия между точками и векторами в пространстве. Действительно, (1,2,5) - это направление или точка?
• Невозможно использовать унифицированный механизм работы с матрицами для выражения преобразований точек. С помощью матриц 3x3 можно описать вращение и масштабирование, однако описать смещение (xў=x+a) нельзя.
• Аналогично, декартовы координаты не позволяют использовать матричную запись для задания перспективного преобразования (проекции) точек.

Для решения этих проблем используются однородные координаты. Существуют различные способы определения однородных координат. Будем исходить из задачи унифицированного представления координат точек в пространстве, включающего бесконечно удаленные точки.

Пусть заданы действительные числа a и w. Рассмотрим их отношение a/w. Зафиксируем значение a, и будем варьировать значение w. При уменьшении w, значение a/w будет увеличиваться. Заметим, что если w стремится к нулю, то a/w стремится к бесконечности. Таким образом, чтобы включить в рассмотрение понятие бесконечности, для представления значения v используется пара чисел (a, w), таких, что v=a/w. Если w не равно 0, значение v в точности равно a/w. В противном случае v = a/0, т.е. равно бесконечности.

Таким образом, координаты трехмерной точки v=(x,y) можно представить через координаты (wx,wy,w). При w=1 эти координаты описывают точку с конечными координатами (x,y), а при w=0 - точку, бесконечно удаленную в направлении (x,y). Как было сказано выше, обычным представлением через декартовы коодинаты (x,y) это сделать невозможно.

Рассмотрим двумерную плоскость, некоторую точку (x,y) на ней и заданную функцию f(x,y). Если заменить x и y на x/w и y/w, то выражение f(x,y)=0 заменится на f(x/w,y/w)=0. Если f(x,y) – многочлен, то его умножение на wⁿ (n – степень многочлена) уберет все знаменатели.

Например, пусть имеется прямая

Замена x и y на x/w и y/w дает A(x/w) + B(y/w) + C = 0. Умножая на w, получаем

Другой пример. Пусть задан многочлен 2-го порядка

После замены x и y на x/w и y/w, соответственно, и умножения на w², получаем

Если внимательно посмотреть на многочлены (1) и (2), можно заметить, что степени при всех членах равны. В случае многочлена 1-го порядка, это степень 1, тогда как для многочлена 2-й степени, все члены (т.е. x², xy, y², xw, yw и w²) имеют степень 2. Следовательно, для данного многочлена n-го порядка, после введения координаты w все члены будут иметь степень n. Такие многочлены называются однородными, а координаты (x,y,w) называются однородными координатами (homogenous coordinates).

Приведенные рассуждения остаются верными и в случае трехмерного пространства. Координаты (x,y,z) заменяются на (x/w, y/w, z/w) и после умножения на w в соответствующей степени n дают однородный многочлен.

Однородные координаты требуют три компоненты для представления точки на плоскости (и четыре компоненты для точки в пространстве). Какие же однородные координаты соответствуют точке с координатами (x,y)? Легко видеть, что это будет (x,y,1), т.е. w полагается равной 1.

В общем случае, это преобразование не однозначно. Однородные координаты точки (x,y) равны (xw, yw,w) для любого ненулевого w. Аналогично в трехмерном пространстве: точке (x,y,z) соответствуют координаты (xw, yw,zw, w). В то же время, преобразование из однородных координат в евклидовы однозначно: точке (x,y,w) соответствует точка (x/w, y/w).

Приведем более формальное определение.

Определение 1 Однородными координатами точки P=(x₁,..,x_n),P О Rⁿ называются координаты P_hom=(wx₁,wx₂,..,wx_n,w),P_hom О Rⁿ⁺¹, причем хотя бы один элемент должен быть отличен от нуля.

На самом деле, множество векторов P_hom при определенных дополнительных операциях образуют так называемое проективное пространство, которое имеет важнейшее значение в машинном зрении. Мы на этом останавливаться не будем. Важнее запомнить следующее: преобразование из однородных координат в евклидовы однозначно; преобразование из евклидовых координат в однородные – нет.

Можно дать простую геометрическую интерпретацию однородных координат на плоскости.

Пусть даны однородные координаты (x,y,w) точки на плоскости Oxy, поставим ей в соответствие точку в трехмерном евклидовом пространстве с координатами x, y и w по осям X, Y и W соответственно. Прямая, соединяющая эту точку c началом координат, пересекает плоскость w=1 в точке (x/w, y/w, 1) (см. рис. 1).

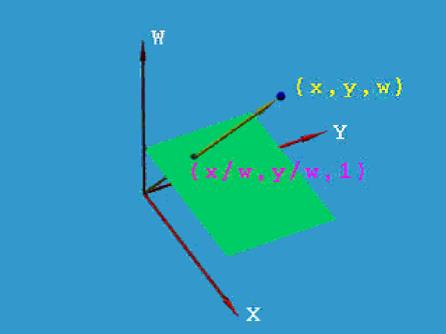
Figure 1: Геометрическая интерпретация однородных координат

Таким образом, преобразование из однородных координат в евклидовы эквивалентно проекции точки на плоскость w=1 вдоль линии, соединяющей точку с началом координат.

Из рисунка также видно, что если преобразование из однородных координат в евклидовы однозначно, то обратное преобразование – нет, потому что все точки на линии, соединяющей точку (x,y,w) и начало координат будут проецироваться в точку (x/w, y/w).

Как было сказано выше, с помощью однородных координат можно легко описывать бесконечность. Рассмотрим точку с однородными координатами (x,y,w). Ей соответствует точка с евклидовыми координатами (x/w, y/w). Зафиксируем x и y и устремим w к нулю. Точка (x/w, y/w) будет удаляться все дальше и дальше в бесконечность в направлении (x,y). Когда w станет нулем, (x/w, y/w) уходит в бесконечность. Следовательно, однородные координаты (x,y,0) – идеальная точка (ideal point) или, по-другому, точка в бесконечности (point at infinity) по направлению (x,y). Аналогично для трехмерного пространства: точка (x,y,z,0) – точка в бесконечности по направлению (x,y,z).

Например, в OpenGL для определения положения источника света используются однородные координаты. С их помощью определить как точечный источник света (w=1), так и параллельный источник света (w=0).