Замечание. На самом деле кривая лежит в объединении выпуклых оболочек, порожденных последовательными наборами из q + 1 точек заданного массива

На самом деле кривая лежит в объединении выпуклых оболочек, порожденных последовательными наборами из q + 1 точек заданного массива. Построенная кривая обладает важным локальным свойством: изменение одной вершины в массиве (или добавление новой вершины к имеющимся) уже не ведет, как прежде, к полному изменению всей кривой:

В силу третьего свойства сохраняется достаточная гладкость кривой: если взять q ³ 4, то все функциональные коэффициенты будут иметь непрерывные вторые производные. Для практических задач большей гладкости, как правило, не требуется. Поэтому обычно ограничиваются рассмотрением случая, когда q = 4.

Замечание Для построения кубического В-сплайна N_i,4(t) требуется 5 узлов разбиения t_i, t_i+1, t_i+2, t_i+3, t_i+4,отрезка [0, 1]. Поэтому если узлов не хватает, то их набор определенным образом расширяют.

Дополнительно введенные отрезки имеют нулевую длину, и первоначальные первый t₀ = 0 и последний t,n = 1 узлы становятся кратными. На рис. 15 показан полный набор кубических В-сплайнов, построенных на расширенном множестве узлов

t_-3 = t_-2 = t_-1 = t₀ = 0;

t₁=0,2; t₂=0,4; t₃=0,6; t₄=0,8;

t_-5 = t_-6 = t_-7 = t₈ = 1.

Замечание

Выбор узлов параметризации может быть совершенно произвольным. Однако часто удобной оказывается параметризация, в которой промежуток изменения параметра t и узлы t_i; определяются длинами соответствующих хорд:

t₀ = 0,

t₁ = ÷V₂V₀÷,

t_i = t_i-1 + |V_i+1, V_i-2÷, i=2.....m-3.

t_m-2 =' t_m-3+|V_m V_m-2|.

Обратимся к следующей достаточно типичной ситуации: по заданному набору точек мы построили В-сплайновую кривую, вывели полученный результат на экран и, внимательно изучив то, что предстало перед глазами, ощутили необходимость подправить кривую в одном или нескольких местах, не изменяя исходного набора точек.

Наиболее подходящим инструментом для подобной процедуры являются числовые или функциональные параметры, заранее введенные в уравнения кривых.

Такую возможность предоставляют некоторые обобщения кубических В-сплайнов, а именно рациональные кубические В-сплайны и бета-сплайны, к описанию которых мы и обратимся.

Рациональные кубические В-сплайны

По заданному набору V₀,V₁,V₂,V₃, рациональная кубическая В-сплайновая кривая определяется уравнением следующего вида:

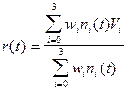, 0 £ t £ 1

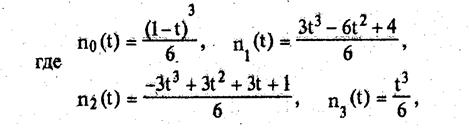
а величины w_i, называемые весами (или параметрами формы), -неотрицательные числа, сумма которых положительна.

Замечания:

1. В случае, если все веса равны между собой, приведенное уравнение описывает элементарную кубическую В-сплайновую кривую.

2. Построение составной рациональной В-сплайновой кубической кривой проводится по той же схеме, что и в полиномиальном случае.

3. В последнее время значительный интерес пользователей вызывает класс сплайнов, известный под названием NURBS - nonuniform rational B'spllnes - рациональных В-сплайнов, задаваемых на неравномерной сетке.