Замечание

При повышении размерности задачи неизбежно возникает значительное число новых проблем. Предложенные ограничения на структуру заданного набора точек (естественно обобщающую структуру плоского сеточного прямоугольника) и выбор в качестве рабочих наиболее простых классов поверхностей дают определенную возможность удержать это число в рамках, разумных для первого знакомства.

Построение сглаживающих поверхностей, как и в рассмотренном выше случае кривых, удобно начать с описания уравнений элементарных фрагментов.

Ограничившись бикубическим случаем (именно такие сплайновые поверхности наиболее часто используются в задачах компьютерной графики), когда функциональные коэффициенты аi(u) и bj(v) представляют собой многочлены третьей степени относительно соответствующих переменных (кубические многочлены), запишем для заданного набора из 16 точек Vy, i=0,l,2,3, j=0,l,2,3, параметрические уравнения элементарных фрагментов некоторых поверхностей, считая для простоты, что область изменения параметров и [у представляет собой единичный квадрат.

Начнем с элементарной бикубической поверхности Безье. Параметрические уравнения фрагмента этой поверхности имеют следующий вид:

,

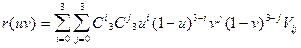0 £ u £ 1, 0 £ v £ 1

или, в матричной форме:

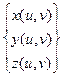= (1 u u² u³) M^T 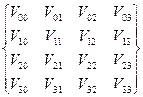M ,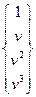

базисная матрица Безье; знаком Т обозначена операция транспонирования.

Элементарная бикубическая поверхность Безье наследует многие свойства элементарной кубической кривой Безье:

лежит в выпуклой оболочке порождающих ее точек;

является гладкой поверхностью;

упираясь в точки V₀₀,V₃₀,V₂₀,V₃₃, касается исходящих из них отрезков контрольного графа заданного набораис.

Из элементарных вырезов поверхностей Безье подобно тому, как это делалось одномерном случае, можно строить составные поверхности.

Остановимся на условиях гладкости таких составных бикубических поверхностей Безье.

Пусть

r = r⁽¹⁾(uv), 0 £ u £ 1, 0 £ v £ 1

и

r = r⁽²⁾(uv), 0 £ u £ 1, 0 £ v £ 1 —

параметрические уравнения двух элементарных бикубических поверхностей Безье, порожденных наборами

V_ij⁽¹⁾, i = 0, 1, 2, 3, j = 0, l, 2, 3, и

V_ij⁽²⁾, i = 0, 1, 2, 3, j = 0, l, 2, 3,

соответственно и такими, что

V_3j⁽¹⁾ =V_0j⁽²⁾, j = 0, l, 2, 3,

Последнее означает, что эти элементарные фрагменты имеют общую граничную кривую.

Поверхность, составленная из этих двух фрагментов, будет иметь непрерывную касательную плоскость, если каждая тройка точек вида

V_2j⁽¹⁾, V_3j⁽¹⁾, = V_0j⁽²⁾, V_1j⁽²⁾,

лежит на одной прямой и, кроме того, отношения

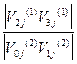
не зависят от номера j (рис. 24)

Векторное параметрическое уравнение элементарного фрагмента бикубической В-сплайновой поверхности, порожденной набором 16 точек V_ij, i = 0, 1, 2, 3, j = 0, l, 2, 3, имеет следующий вид:

r(u,v) = 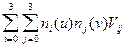0 £ u £ 1, 0 £ v £ 1

(функциональные. коэффициенты n₀, n₁, n₂, n₃ те же, что и выше), в матричной форме,

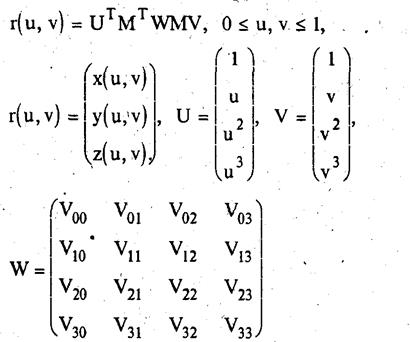
Здесь М - базисная матрица кубического В-сплайна.

Как и бикубическая поверхность Безье, элементарная бикубическая В-сплайновая поверхность наследует многие свойства элементарной кубической В-сплайновой кривой:

• является гладкой;

• лежит в выпуклой оболочке порождающих ее 16 вершин;

• "повторяет" контрольную многогранную поверхность.

Построение составной бикубической В-сплайновой поверхности (обладающей весьма привлекательными геометрическими свойствами) на прямоугольнике [0, m] х [0, n] с равномерными узлами (i, j), i = 0,1,..., m -1, m, j = 0,1,..., n -1, n, проводится во многом подобно тому, как это делается в одномерном случае.

Разумеется, существуют и весьма эффективно используются двумерные аналоги и рациональных В-сплайновых кривых (как на равномерной сетке, так и на неравномерной (NURBS)).

Мы остановились в этой главе лишь на некоторых простых способах построения плавно изменяющихся кривых и поверхностей.

К сказанному следует также добавить, что построение искривленных пространственных объектов является действительно непростой задачей. Она требует достаточно развитого пространственного воображения и почти постоянной готовности к встрече с вещами неожиданными. Хотя и объяснимыми, не сразу, а после заметных усилий. Тем не менее мы стремились к тому, чтобы по отобранному материалу и программным реализациям представленных алгоритмов у читателя сложилось в целом правильное начальное представление о геометрических сплайнах и том месте, которое они занимают в компьютерной графике.

По нашему мнению, даже небольшая самостоятельная попытка компьютерной реализации высказанных здесь сравнительно несложных геометрических соображений будет, несомненно, полезна в освоении практически неисчерпаемых возможностей компьютерной графики.