2015-05-30
1340
Теорема 1
Если функци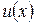и 
и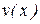 
имеют производные во всех точках интервала 
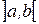, то производная их алгебраической суммы равна алгебраической сумме производных, то есть 
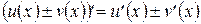для любого 
.
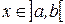Доказательство: рассмотрим функцию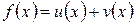 
, где 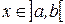и найдем производную этой функции, исходя из определения. Пусть 
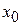– некоторая точка интервала 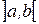. Тогда
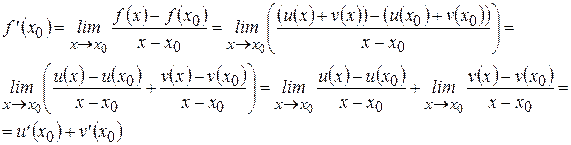
Итак,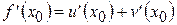 
.
Так как 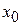– произвольная точка интервала 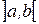, то имеем
.
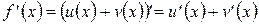Случай разности рассматривается аналогично. Теорема доказана.
Примеры: Найти производную:
1) 
;
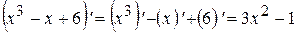2) 
;
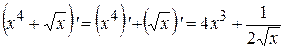Замечание: Данная теорема справедлива для любого числа слагаемых.
