2015-05-30
778
Установим необходимое условие существования производной.
Теорема:
Если функция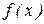 
имеет производную в точке 
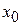, то она непрерывна в этой точке.
Доказательство: Любому значению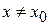 
, взятому из области определения функции 
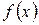, соответствует приращение аргумента 
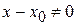и некоторое приращение функции 
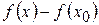. Рассмотрим тождество:
.
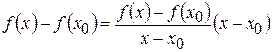Переходя к пределу при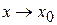 
в этом тождестве, получаем:
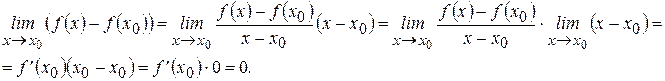Следовательно, 
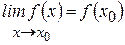, что и означает непрерывность функции 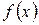в .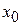
Замечание: Из доказанной теоремы следует, что если функция не является непрерывной в некоторой точке, то она в этой точке не имеет производной, то есть непрерывность в точке – необходимое условие дифференцируемости в точке. Однако, следует заметить, что непрерывность функции в точке не является достаточным условием существования производной этой функции в рассматриваемой точке, то есть из непрерывности функции в точке не следует ее дифференцируемость в этой точке.
Пример: Функция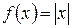 
непрерывна в любой точке числовой оси, в том числе и в точке 
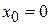(рис. 3)
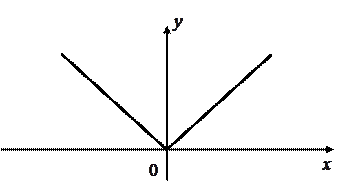
Рис. 3
Однако в точке 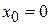данная функция не имеет производной. В самом деле: 
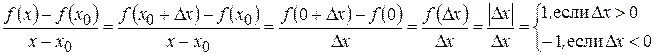Отсюда следует, что предел 
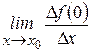не существует (так как, если предел существует, то только один) и, следовательно, не существует производной функции 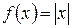в точке .
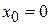Таким образом, существует функции, всюду непрерывные, но не имеющие производных в некоторых точках.
