Если функция 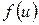 дифференцируема по
дифференцируема по 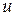 , а функция
, а функция 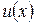 дифференцируема по
дифференцируема по 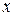 , то производная сложной функции
, то производная сложной функции 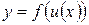 по независимой переменной
по независимой переменной 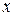 определяется равенством:
определяется равенством: 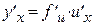 .
.
Доказательство: Пусть дана дифференцируемая функция 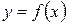 , которая является сложной и имеет промежуточный аргумент
, которая является сложной и имеет промежуточный аргумент 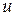 зависящий от
зависящий от 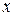 .
.
По определению производной можем записать 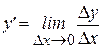 . Умножив числитель и знаменатель функции, содержащейся под знаком предела, на приращения промежуточного аргумента
. Умножив числитель и знаменатель функции, содержащейся под знаком предела, на приращения промежуточного аргумента 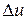 , получим:
, получим:
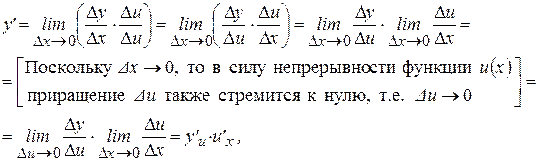
то есть
производная сложной функции 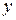 по аргументу
по аргументу 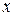 равна производной этой функции по промежуточному аргументу
равна производной этой функции по промежуточному аргументу 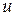 , умноженной на производную внутренней функции
, умноженной на производную внутренней функции 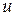 по основному аргументу
по основному аргументу 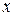 .
.
Это правило иногда называют правилом цепочки: то есть производная сложной функции равна произведению производных от всех составляющих ее функций. При этом следует помнить, что каждую функцию нужно дифференцировать по ее собственному аргументу.
Пример: Найти производную функции: 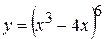 .
.
Решение: Эта функция сложная, то есть 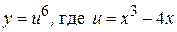 .
.
Согласно правилу дифференцирования сложной функции получим: 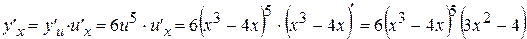 .
.
 2015-05-30
2015-05-30 848
848








