Исходя из определения производной, сформулируем правило нахождения производной функции в точке:
Чтобы вычислить производную функции 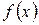 в точке
в точке 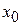 нужно:
нужно:
1. Найти разность 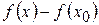 ;
;
2. Найти отношение 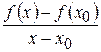 ;
;
3. Найти предел этого отношения при 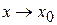
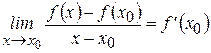 .
.
Пример 1: Найти производную функции 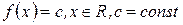 .
.
Решение:
1) Находим разность: 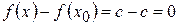 .
.
2) Находим отношение: 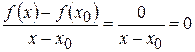 .
.
3) Находим предел: 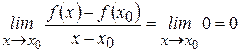 .
.
Получили, что 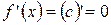 .
.
Вывод: Производная постоянной равно нулю.
Пример 2: Найти производную функции 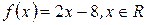 .
.
Решение:
1) Находим разность: 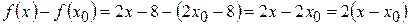 .
.
2) Находим отношение: 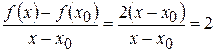 .
.
3) Находим предел: 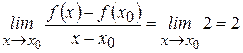 .
.
Получили, что 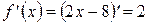 .
.
Пример 3: Найти производную функции 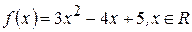 .
.
Решение:
1) Находим разность:
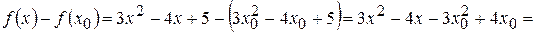
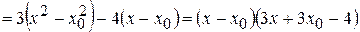
2) Находим отношение:
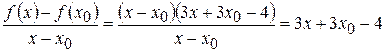 .
.
3) Находим предел:
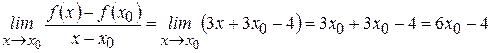
Таким образом 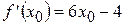 . Так как функция
. Так как функция 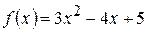 имеет производную в любой точке
имеет производную в любой точке 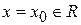 , то будем писать
, то будем писать 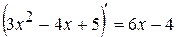 .
.
 2015-05-30
2015-05-30 2348
2348
