Если функции 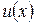 и
и 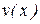 имеют производные во всех точках интервала
имеют производные во всех точках интервала 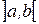 , то
, то 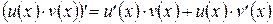 для любого
для любого 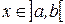 .
.
Доказательство: рассмотрим функцию 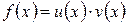 , где
, где 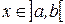 и найдем производную этой функции, с помощью определения. Пусть
и найдем производную этой функции, с помощью определения. Пусть 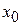 – произвольная точка интервала
– произвольная точка интервала 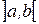 . Тогда
. Тогда
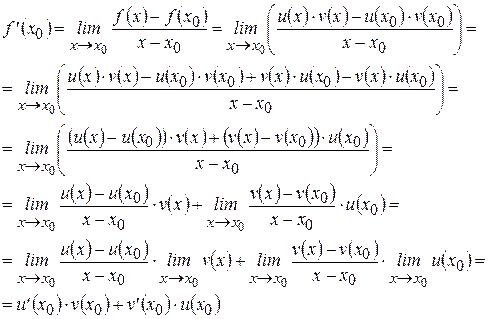
Итак, 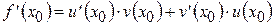 .
.
Так как 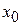 – произвольная точка интервала
– произвольная точка интервала 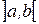 , то имеем
, то имеем
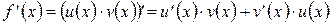 .
.
Примеры:
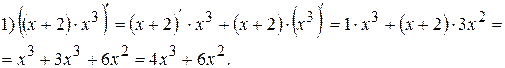
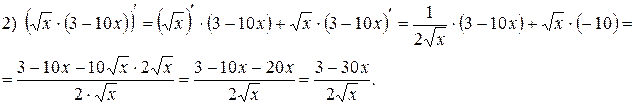
Следствие: Постоянный множитель можно выносить за знак производной:
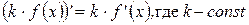
Доказательство: Применим теорему о производной произведения:
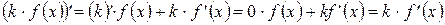 .
.
Примеры:
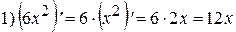 ;
;
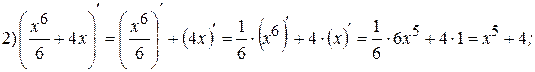
Теорема 3:
Если функции 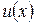 и
и 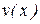 имеют производные во всех точках интервала
имеют производные во всех точках интервала 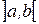 , причем
, причем 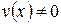 для любого
для любого 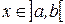 , то
, то 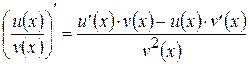 для любого
для любого 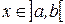 .
.
Доказательство: Рассмотрим функцию 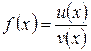 , где
, где 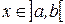 и найдем ее производную, пользуясь определением. Пусть
и найдем ее производную, пользуясь определением. Пусть 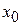 – произвольная точка интервала
– произвольная точка интервала 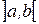 . Тогда
. Тогда
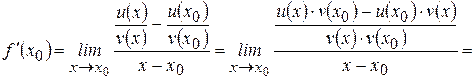
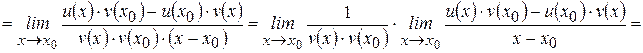
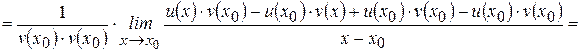
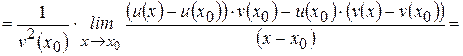
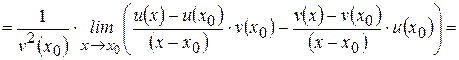
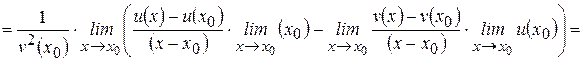
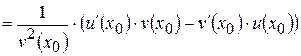 .
.
Следовательно,
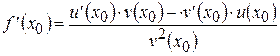 .
.
А так как 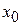 – произвольная точка интервала
– произвольная точка интервала 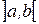 , то имеем
, то имеем 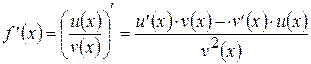 .
.
Примеры:
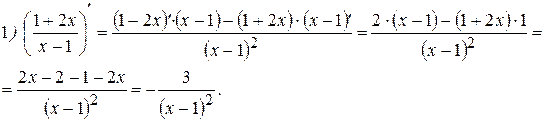

 2015-05-30
2015-05-30 689
689








