2015-05-30
701
В параграфе 1 шла речь о мгновенной скорости движения и о мгновенной силе тока. Введение этих понятий происходило с помощью некоторого предела. Можно привести еще не мало задач, для которых также необходимо находить скорость изменения некоторой функции, например нахождение теплоемкости тела при нагревании, угловой скорости вращающегося тела и др.
I Рассмотрим функцию f(x), xÎ[a;b]
Возьмем произвольную точку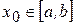 
. Тогда для любого 
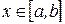разность 
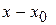называется приращением аргумента 
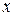в точке 
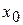и обозначается 
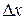, то есть 
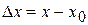. Разность 
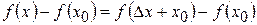называется приращением функции 
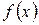в точке 
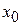и обозначается 
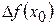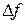(или 
, или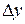 
), то есть
.
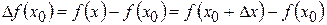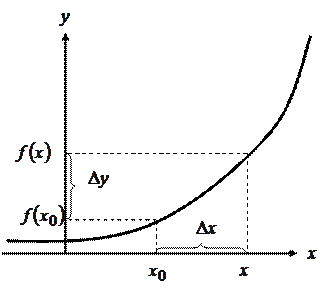
Рис. 2
Производной функции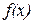 
в точке 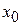называется предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, если этот предел существует, то есть
.
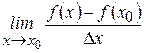Производная функции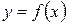 
в точках 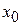обозначается: 
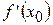или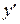 
(читается: «эф штрих от икс 0» или «игрек штрих»).
Итак, по определению получим, что
.
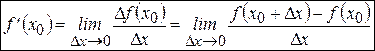Часто для обозначения производной используется символ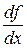 
или 
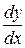(читается «де эф по де икс» или «де игрек по де икс»).
Операция нахождения производной от данной функции называется дифференцированием.
Функция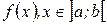 
, имеющая производную в каждой точке интервала 
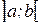, называется дифференцируемой на этом интервале.
