Вначале выведем формулу дифференцирования функции 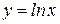 , где
, где 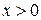 .
.
Найдем производную с помощью определения:
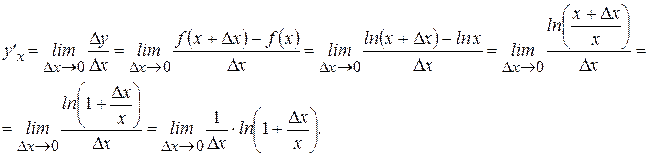
Теперь функцию, содержащуюся под знаком предела, умножим и разделим на 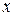 (это можно сделать, так как
(это можно сделать, так как 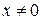 ), а затем воспользуемся свойством логарифмов:
), а затем воспользуемся свойством логарифмов: 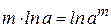 , получим
, получим
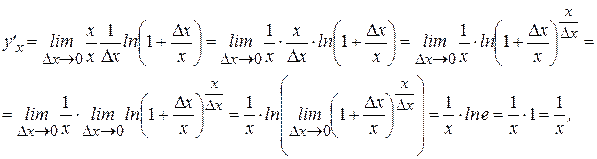
так как
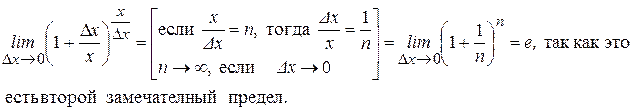 Итак получили, что
Итак получили, что
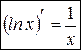 . (1)
. (1)
Выведем теперь формулу дифференцирования сложной функции, то есть функции 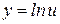 , где
, где 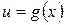 . Для этого используем формулу дифференцирования сложной функции
. Для этого используем формулу дифференцирования сложной функции 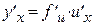 , получим:
, получим:
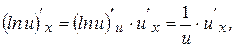 то есть
то есть
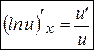 . (1’)
. (1’)
Пример: Найти производные следующих функций:
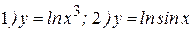
Решение:
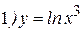
Первый способ:
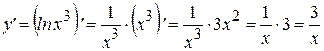 ;
;
Второй способ:
Вначале преобразуем функцию с помощью свойств логарифмов:
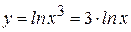 .
.
А теперь найдем производную:
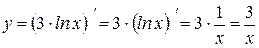 ;
;
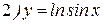
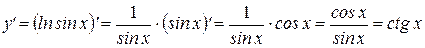
Найдем теперь производную функции 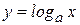 , где
, где 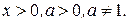
Для того, чтобы найти производную функции 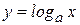 , воспользуемся формулой перехода от логарифма с одним основанием, к логарифму с другим основанием:
, воспользуемся формулой перехода от логарифма с одним основанием, к логарифму с другим основанием: 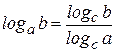 , где
, где 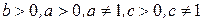 и перейдем от логарифма с основанием a к логарифму с основанием e, получим:
и перейдем от логарифма с основанием a к логарифму с основанием e, получим:
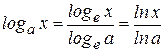
А теперь найдем производную функции 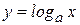 :
:
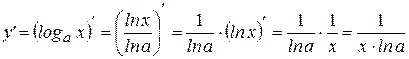
Получим, что
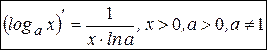 . (2)
. (2)
Теперь найдем производную сложной функции 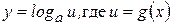 . Воспользуемся правилом дифференцирования сложной функции, получим:
. Воспользуемся правилом дифференцирования сложной функции, получим:
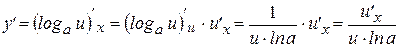 , то есть
, то есть
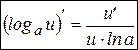 . (2’)
. (2’)
Пример: Найти производные следующих функций:
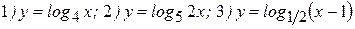
Решение:
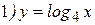
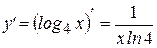
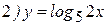
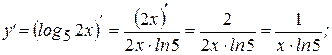
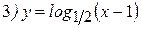
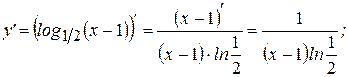
Замечание: При нахождении производной логарифмической функции иногда проще вначале преобразовать функцию, пользуясь свойствами логарифма, а только затем находить производную. Поэтому напоминаем основные свойства логарифмической функции:
1) 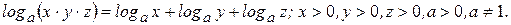
2) 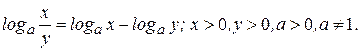
3) 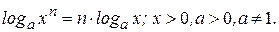
4) 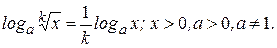
Пример: Найти производную функции: 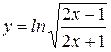 .
.
Решение: Вначале преобразуем функцию:
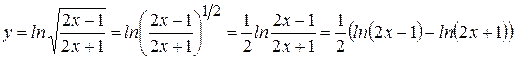
А теперь найдем производную:
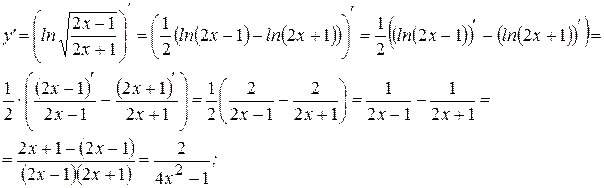
 2015-05-30
2015-05-30 2412
2412
