1).Определение скорости точки. Вектор скорости точки 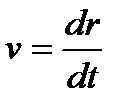 . Отсюда, учитывая, что
. Отсюда, учитывая, что 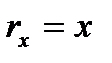 ,
, 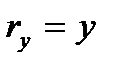 ,
, 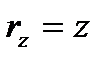 , будем иметь:
, будем иметь: 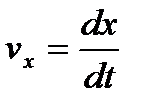 ,
, 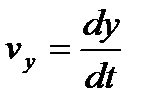 ,
, 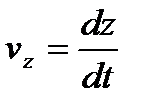 , или
, или 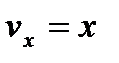 ,
, 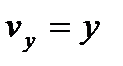 ,
, 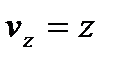 , где точка над буквой есть символ дифференцирования по времени. Таким образом, проекции скорости точки на оси координат равны первым производным от соответствующих координат точки по времени
, где точка над буквой есть символ дифференцирования по времени. Таким образом, проекции скорости точки на оси координат равны первым производным от соответствующих координат точки по времени 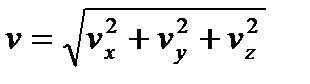 . 2). Определение ускорения точки. Вектор ускорения точки
. 2). Определение ускорения точки. Вектор ускорения точки 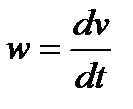
 . Отсюда на основании теоремы о проекции производной и формул получаем:
. Отсюда на основании теоремы о проекции производной и формул получаем: 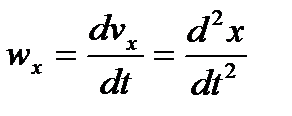 ,
, 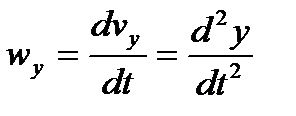 ,
, 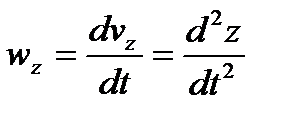 ,
, 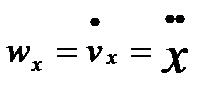 ,
, 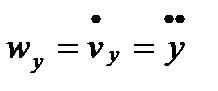 ,
, 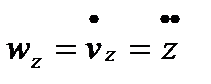 , т.е. проекции ускорения точки на оси координат равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени
, т.е. проекции ускорения точки на оси координат равны первым производным от проекций скорости или вторым производным от соответствующих координат точки по времени 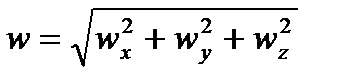 .
.
Определение скорости и ускорения точки при координатном способе задания движения.С.149
|
|

Сейчас читают про:
 2015-05-30
2015-05-30 782
782







