Для атрибутивных признаков

Если изучаемые атрибутивные признаки имеют больше двух значений, то применяют коэффициенты корреляции Пирсона и Чупрова.

Для данных коэффициентов необходимо составить таблицу взаимной сопряженности:

Таблица сопряженности

Значения Х	Значения Y
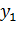
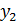
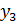
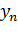
			…		Сумма по строке (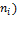
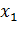
	n11	n12	n13	…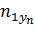
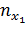
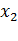
	n21	n22	n23	…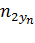
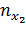
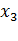
	n31	n32	n33	…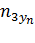
…	…	…	…	…
				…
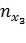
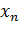
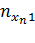
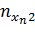
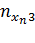
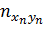
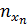
Сумма по столбцу (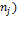

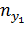
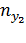
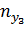
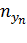
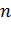
Частоты, стоящие в клетках таблицы, называются клеточными частотами.

Факт наличия связи устанавливается с помощью критерия χ².

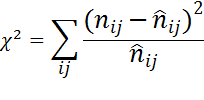
Где 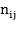- фактическая клеточная частота, т.е. число единиц наблюдения с i-ым значением признака Х и j-ым значением признака Y;

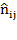- теоретическая клеточная частота (при равенстве фактических и теоретических частот связь между Х и Y отсутствует)

Теоретические частоты для каждой клетки вычисляются по формуле

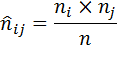
Величина 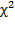показывает насколько велика разница между фактическими клеточными частотами и теми частотами, которые были бы, если бы между переменными не было связи. Эта разница всегда будет, поэтому полученную величину 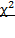нужно сравниватьс минимально допустимой величиной из таблицы критических значений 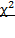. На величину 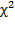влияет число степеней свободы и уровень значимости .

Число степеней свободы определяется следующим образом

,

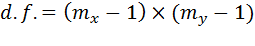Где 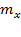– количество групп фактора X, 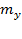– количество групп фактора Y.

Таблица критических значений 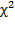приведена в конце лекции.

Выбираем по таблице значение 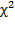, соответствующее рассчитанной ранее степени свободы и уровню значимости.

Если рассчитанное по формуле значение 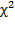превышает табличное значение 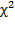, то связь между X и Y подтверждается (т.е. корреляционная связь между Х и Y присутствует).

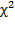подтверждает только наличие связи.

Тесноту связи определяют при помощи коэффициентов взаимной сопряженности.