1. Функция F(x) называется первообразной для функции f(x) на (a; b), если для любого 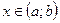 выполняется равенство
выполняется равенство
| Варианты ответов: | |||
| 1) | F(x)=f(x) | 2) | 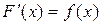 |
| 3) | 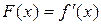 | 4) | 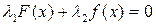 |
2. Какое из свойств определенного интеграла не имеет места?
| Варианты ответов: | |||
| 1) | 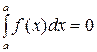 | 2) | 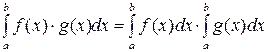 |
| 3) | 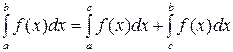 | 4) | 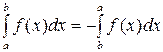 |
3. Какой интеграл вычислен верно?
| Варианты ответов: | |||
| 1) | 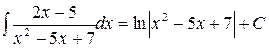 | 2) | 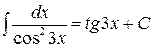 |
| 3) | 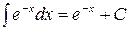 | 4) |  |
4. В интеграле 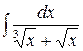 для приведения подынтегральной функции к рациональной дроби необходима подстановка
для приведения подынтегральной функции к рациональной дроби необходима подстановка
| Варианты ответов: | |||
| 1) | 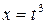 | 2) | 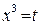 |
| 3) | 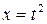 | 4) | 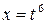 |
5. Объем тела, образованного вращением кривой 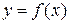 вокруг оси OY можно вычислить по формуле:
вокруг оси OY можно вычислить по формуле:
| Варианты ответов: | |||
| 1) | 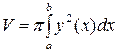 | 2) | 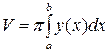 |
| 3) | 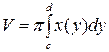 | 4) | 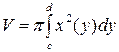 |
6. Вычислить 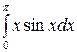
| Варианты ответов: | |||
| 1) | 2) | -1 | |
| 3) | 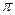 | 4) | - 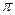 |
7. Среди дробей укажите правильные
1) 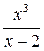 ; 2)
; 2) 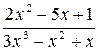 ; 3)
; 3) 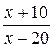 ; 4)
; 4) 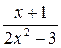 .
.
| Варианты ответов: | |||
| 1) | 1 и 3 | 2) | 2 и 4 |
| 3) | 1 и 2 | 4) | 3 и 4 |
8. Для вычисления интеграла 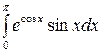 целесообразно сделать подстановку cosx=t. При этом пределы нового интеграла будут
целесообразно сделать подстановку cosx=t. При этом пределы нового интеграла будут
| Варианты ответов: | |||
| 1) | а=1, b=-1 | 2) | a=0, b=1 |
| 3) | a=-1, b=1 | 4) | a=1, b=0 |
9. Укажите функцию f(x), первообразная которой 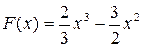
| Варианты ответов: | |||
| 1) | f(x)=4x-3 | 2) | 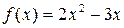 |
| 3) | 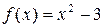 | 4) | 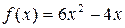 |
10. Вычислить 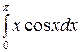
| Варианты ответов: | |||
| 1) | 2) | 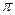 | |
| 3) | 4) | -2 |
11. Если 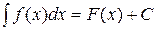 , то справедливо равенство
, то справедливо равенство
| Варианты ответов: | |||
| 1) | 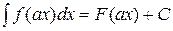 | 2) | 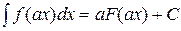 |
| 3) | 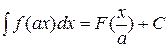 | 4) | 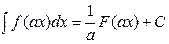 |
12. Для вычисления площади фигуры, ограниченной линией 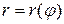 пользуются формулой:
пользуются формулой:
| Варианты ответов: | |||
| 1) | 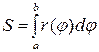 | 2) | 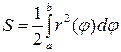 |
| 3) | 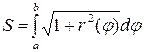 | 4) | 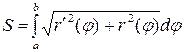 |
13. Разложение дроби 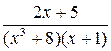 на простейшие имеет вид
на простейшие имеет вид
| Варианты ответов: | |||
| 1) | 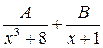 | 2) | 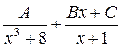 |
| 3) | 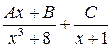 | 4) | 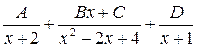 |
14. Какой из интегралов вычислен верно?
| Варианты ответов: | |||
| 1) | 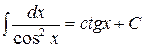 | 2) | 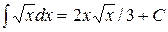 |
| 3) | 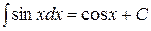 | 4) | 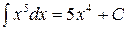 |
15. Какое из свойств неопределенного интеграла не имеет места?
| Варианты ответов: | |||
| 1) | 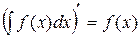 | 2) | 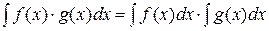 |
| 3) | 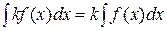 | 4) | 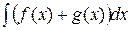 = = 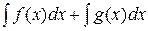 |
16. Формула интегрирования по частям имеет вид
| Варианты ответов: | |||
| 1) | 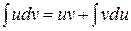 | 2) | 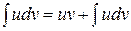 |
| 3) | 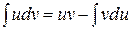 | 4) | 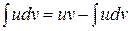 |
17. Определенным интегралом от непрерывной на отрезке [a;b] функции f(x) называется
| Варианты ответов: | |||
| 1) | 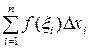 | 2) | 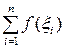 |
| 3) | 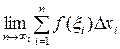 | 4) | 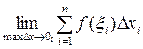 |
18. Формула Ньютона-Лейбница имеет вид
| Варианты ответов: | |||
| 1) | 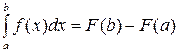 | 2) | 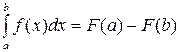 |
| 3) | 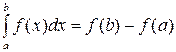 | 4) | 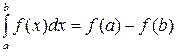 |
19. Интеграл 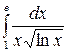 равен
равен
| Варианты ответов: | |||
| 1) | 2) | ∞ | |
| 3) | 0,5 | 4) |
20. Длину дуги кривой 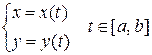 можно найти по формуле
можно найти по формуле
| Варианты ответов: | |||
| 1) | 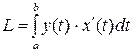 | 2) | 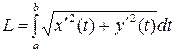 |
| 3) | 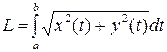 | 4) | 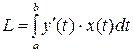 |
 2015-05-30
2015-05-30 8399
8399







